Пусть (x1) и (x2) - корни уравнения 4x^2-6x-1=0.
Составьте квадратное уравнение, корнями которого являются число (y1)=(2/(x1)^3)-1
(y2)=(2/(x2)^3)-1
Приложения:
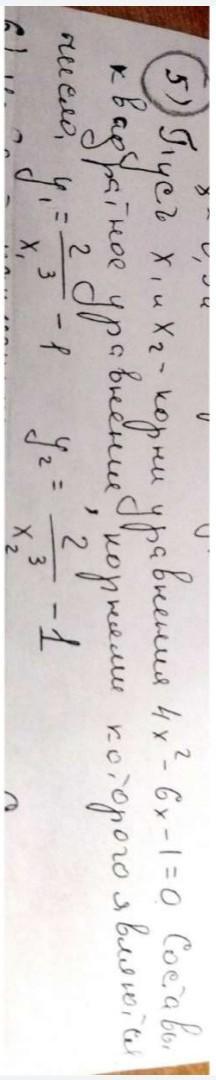
Ответы
Ответ дал:
2
1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
Ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
Ответ дал:
1
Объяснение: см. во вложение
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад