Докажите неравенство:
Приложения:
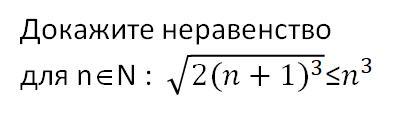
igorShap:
И тут тоже: n=1=> 4≤1. Опять не вся информация, как минимум, предоставлена
Хотя дальше, по идее, все выполняется
Это устанавливается в процессе решения как часть решения, не так ли?
Нет, извините, в условии четко прописано: доказать неравенство для натуральных значений n. Если есть контрпример - неравенство уже не тождественно верно.
Хорошо.
тут для n>=2...
неравенство достаточно просто сводится к неравенству 2^{1/6}<=sqrt{(n^2)/(n+1)}, причем эта функция монотонна
для натуральных значений
Пожалуйста, приведите доказательство. Благодарю
Ответы
Ответ дал:
2
Для выражение
положительно. Сделаем преобразования, эквивалентные на данном множестве:
.
Пусть строго монотонные непрерывные функции (и дифф. на рассматриваемом множестве). Тогда
тоже монотонна на этом множестве. Достаточно показать, что
не имеет корней:
, где каждое из множителей не обращается в нуль на рассматриваемом множестве. (Поправьте, если неправ).
Рассмотрим функцию . Докажем, что она монотонна при положительных
:
.
Используя вышеизложенные рассуждения, приходим к выводу: монотонна при положительных значениях
. (Можно и проще: просто поделить на
числитель и знаменатель).
Для имеем:
.
Спасибо. Идеальное решение. Остается адаптировать для десятиклассника, который еще не учил производную...
ну вот поделив числитель и знаменатель на n^2 получаем sqrt(1/(1/n+1/n^2)). теперь достаточно понимать, что корень монотонен, сумма монотонных монотонна и т.д., без производных
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад