Question

Стороны выпуклого четырехугольника MNKL равны MN = a, NK = b, KL = c, ML = d. Найдите площадь четырехугольника MNKL, если известно, что существуют такие точки А и В, где A принадлежит МL, B принадлежит NK, что вокруг четырехугольников MNBA и KLBA можно описать окружности

Answer 1

Ответ: Формула на рисунке

Объяснение:

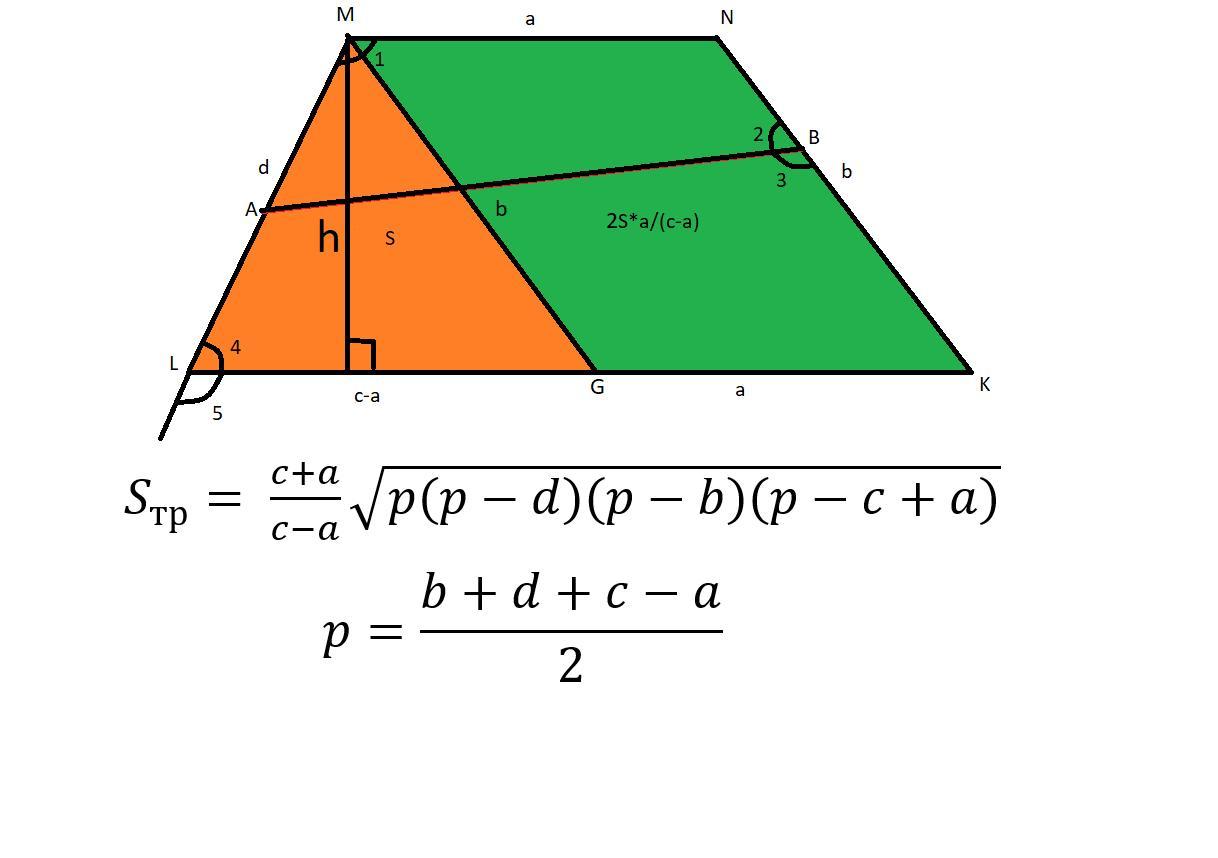
Из условия того, что вокруг  четырехугольников MNBA и KLBA можно описать окружности имеем (cмотрите рисунок)

∠1+∠2 = 180°

∠3 +∠4 =180°

Сложим эти два равенства :

∠1 +∠4 +∠2 +∠3 =360°

∠2+∠3 = 180° → ∠1 +∠4 = 180° → ∠5 =∠1 → MN║LK → MNKL - трапеция с основаниями a и c.

Проведем MG║NK, тогда MGKN - параллелограмм.

MN=GK=a → LG= c-a

MG=NK=b

Обозначим площадь ΔLMG как S ( она может быть рассчитана по формуле Герона)

Тогда высота трапеции:

h=2S/(c-a) →  SMGKN = 2S*a/(c-a)

Тогда площадь трапеции:

Sтр = S + 2S*a/(c-a) = (1 + 2a/(c-a) )*S = S*(c+a)/(c-a)

Формула площади с учетом формулы Герона показана на рисунке.