Question

Вершину A трапеции ABCD соединили с серединой боковой стороны CD. Площади полученных четырёхугольника и треугольника равны 5 и 2 соответственно. Найдите отношение меньшего основания этой трапеции к большему основанию.

Answer 1

Ответ:

3 : 4

Объяснение:

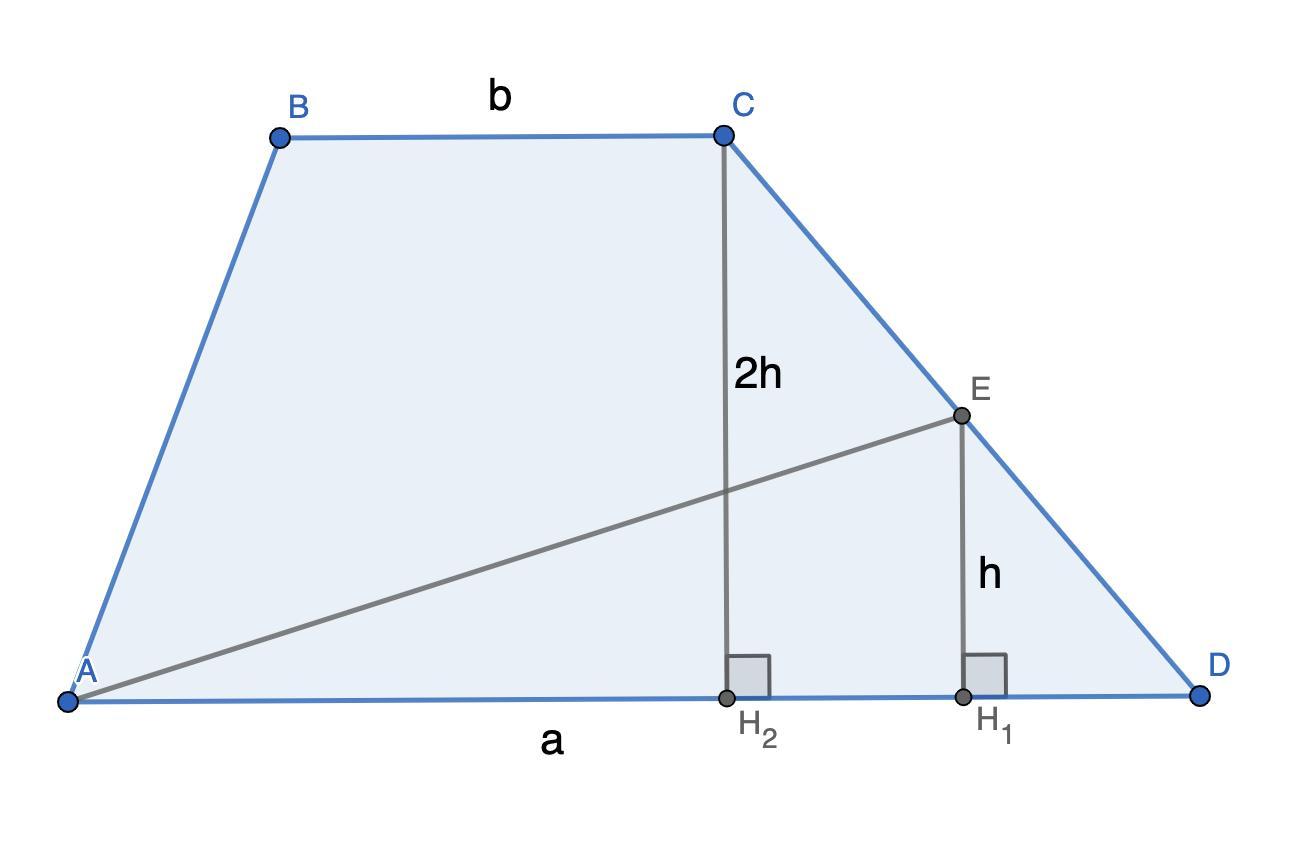
Пусть E — середина CD. Проведём высоты EH₁ и CH₂. Обозначим AD = a, BC = b, EH₁ = h. Для треугольника CH₂D EH₁ — средняя линия (EH₁ || CH₂, CE = ED) ⇒ CH₂ = 2h.

$S_{AED}=\dfrac{ah}{2}=2\Leftrightarrow ah=4\\S_{ABCE}=S_{ABCD}-S_{AED}=\dfrac{a+b}{2}\cdot 2h-2=5\Leftrightarrow ah+bh=7\Leftrightarrow 4+bh=7\\bh=3\\\dfrac{bh}{ah}=\dfrac{b}{a}=\dfrac{3}{4}$