Найти наименьшее значение выражения (без использования производной)
Приложения:
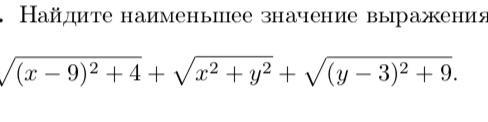
Аноним:
(9;3)
не так все просто
автору спасибо за красивый вопрос.
Автор вопроса и есть автор метода решения ВБ
что дает использования производной ?
Наименьшее значение выражения получается, если слагаемые будут равны , дальше ?
Выражение зависит от х и от y. Функция двух переменных. Производные - частные производные.
Понятно , что частные производные, но рационально ?
Нет
Ответы
Ответ дал:
3
решение по методу одного участника ресурса ВБ
для нахождения Минимума √((х - 9)² + 4) + √(x² + y²) + √((y - 3)² + 9)
будем использовать вектора
Пусть a = {9 - x, 2}
b = {x, y}
c = {3, 3 - y} (Над a b c - стрелочки)
тогда |a| = √((х - 9)² + 4)
|b| = √(x² + y²)
|c| = √((y - 3)² + 9)
Суммируем
(a + b + c) = {9 - x + x + 3, 2 + y + 3 - y} = {12, 5}
|a + b + c| = √(12² + 5²) = √13² = 13
так как |a| + |b| + | c| ≥ |a + b + c| то минимум = 13
ответ 13
здорово. Но Вы это озвучили. Еще раз спасибо!
Вектора должны быть параллельны, отсюда находим x и y
в решении ничего не указано. было бы неплохо довести до совершенства
я вам освободил второе окно - пожалуйста
Решение классное, Вектора рисовал, но до главной идеи не дошел.
Самый красивый способ геометрический, рассматриваем суммы гипотенуз трех прямоугольных треугольников. Cумма гипотенуз минимальна, когда гипотенузы всех треугольников лежат на одной прямой, то есть когда треугольники подобны.
Но векторы тоже неплохо.
хотите решить ?
Сейчас нет времени. Уже решал похожее задание таким способом. Где то было в моих решенных задачах
будет время напишите - создам вопрос
было бы хорошо
было бы хорошо
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад