Question

четырёхугольник ABCD является одновременно вписанным и описанным.Пусть M,N,P и Q-точки касания вписанной окружности со сторонами четырехугольника.Докажите что MP перпендикулярен NQ

Answer 1

Ответ:

Дуги MQN и QMP, если подумать равны 540 градусам, тк их градусная мера равна 2 кругам, из которых вырезали 180 градусов (как раз сумму углов MBN и QDP)

Объяснение:

Answer 2

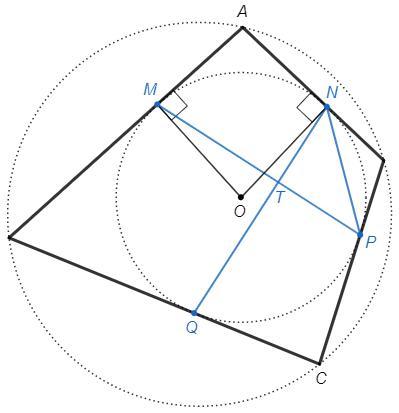
O - центр вписанной окружности.

Радиус в точку касания перпендикулярен касательной.

OMA=ONA=90 => A+O=180 => A+∪MN=180

Аналогично С+∪PQ=180

Сумма противоположных углов вписанного четырехугольника 180.

A+C=180 => ∪MN+∪PQ=180 => MPN+PNQ=90 => T=90