Решите подробно,пожалуйста)
Приложения:
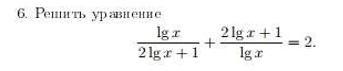
Аноним:
Найди ОДЗ, замени lgx на t, реши уравнение. Получишь t = -1, от куда lgx = -1, x = 10^(-1) = 1/10. Ответ : 1/10
Ответы
Ответ дал:
1
ОДЗ:
{x>0
{2lgx+1≠0
{lgx≠0
Замена переменной:
тогда
Уравнение:
⇒ t=1
Обратная замена
⇒
удовл ОДЗ
О т в е т. 0,1
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад