Ответы
Ответ дал:
1
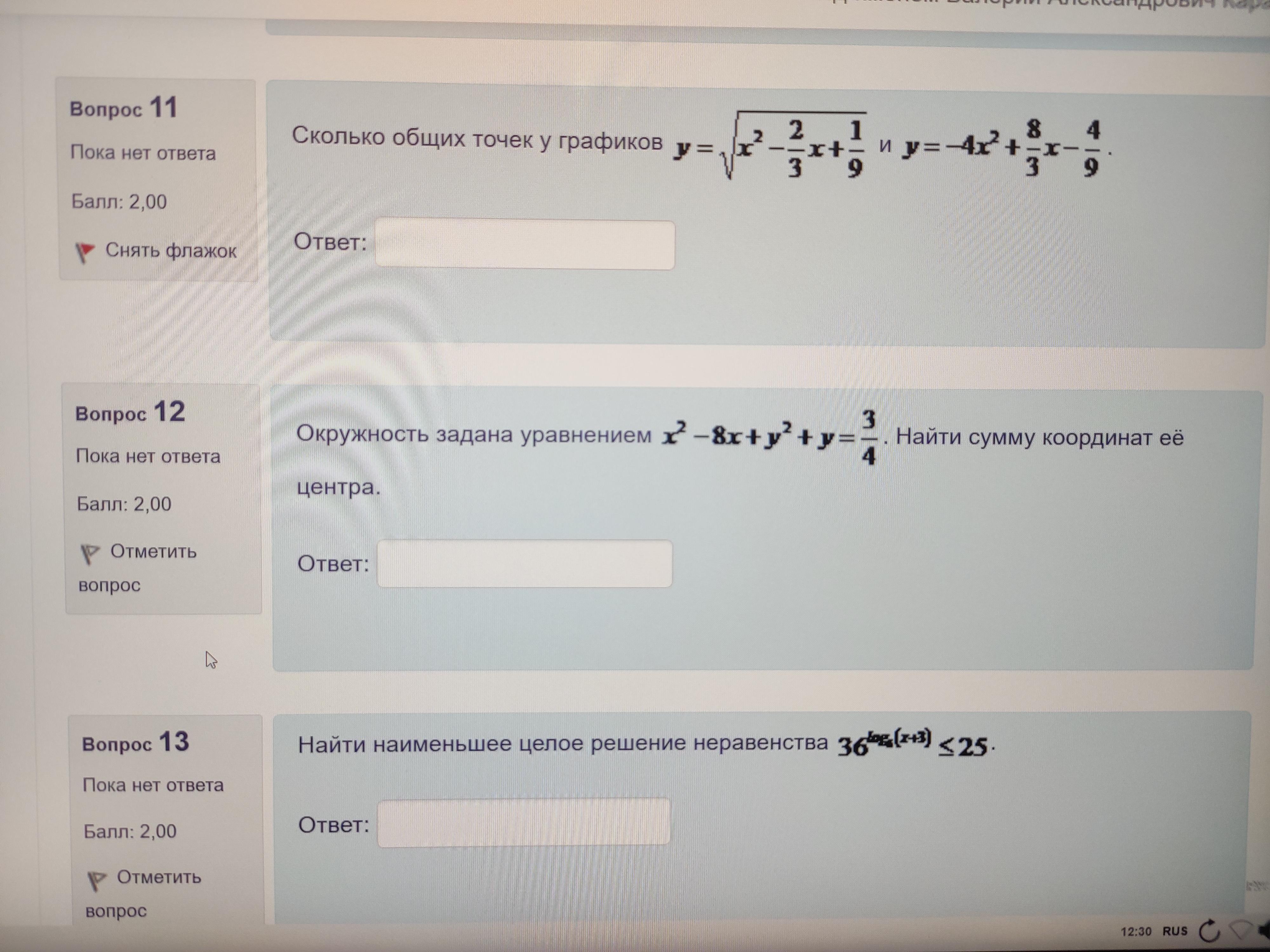
11. Для нахождения общих точек приравняем ординаты функций:
Заметим, что правая части при любых x, а левая -
при любом x. Соответственно, равенство может достигаться только тогда, когда обе части одновременно равны 0 - очевидно, что это происходит при
.
Теперь понятно, что графики функций имеют одну общую точку.
12. В левой части выделим полные квадраты:
Последнее уравнение задает окружность с центром в точке (4; -0,5) и радиусом
Сумма координат центра равна 4 + (-0,5) = 4 - 0,5 = 3,5.
13. На ОДЗ - x + 3 > 0 ⇒ x > -3, имеем:
Итого имеем неравенство
С учетом ОДЗ получаем ответ:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад