Предмет: Геометрия
Автор: Nurzhan94
Вопрос задан 3 года назад

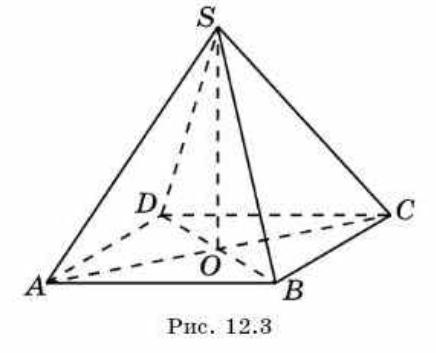
найдите высоту правильной четырехугольной пирамиды SABCD все ребра которой равны 1

Приложения:

Аноним: В основании квадрат. Диагональ квадрата равна,по теореме ПифагораАС=√(АВ²+ВС²)=√(1²+1²)=√2. Половина диагонали равно ОС=АС/2=√2/2. Высота пирамиды по теореме Пифагора равна OS=√(SC²-OC²)=√(1²-(√2/2)²)=√(1-2/4)=√(1-1/2)=√1/2=1/√2

Ответы

Ответ дал: Кремская

Так как по условию задачи пирамида правильная, то в основании – квадрат. Диагональ квадрата равна произведению его стороны на √2, то есть d = √2·а

а = AB=BC=CD=AD = 1 (ед.измер.) по условию задачи

d = АС = BD = √2 · 1 = √2

Половина диагонали АО = AS/2 = √2/2

По условию задачи все рёбра пирамиды равны, поэтому SA = SB = SC = SD = 1 (ед.измер.) Из прямоугольного ΔAOS:

SO = √АS² - АО² = √1² - (√2/2)² = √2/2

Ответ: √2/2 (ед.измер.)

Аноним: ???? 1²-(√2/2)²=1-2/4=4/4-2/4=2/4=1/2 отсюда √(1/2)???

Кремская: 1/√2 =√2/2 Избавляемся от иррациональности в знаменателе. Умножаем числитель и знаменатель на √2, таким образом получается 1*√2 / √2*√2 = √2/2

Аноним: Ага, спасибо...

Вас заинтересует

Математика

2 года назад

Упражнение 3.На кр не смог объясните пж пересдавать пойду

Математика

2 года назад

Сергей и Андрей собрали 6,4 кг малины. Сколько килограммов малины собрал Андрей, если он собрал на 0,4 кг малины меньше, чем Сергей?

Українська мова

2 года назад

зробити аналіз слова електричний 1аналізоване слово 2від якого слова в реченні залежить 3на яке питання відповідає 4до якої частини мови належить 5число 6 рід в однині 7 яким є членом речення

Информатика