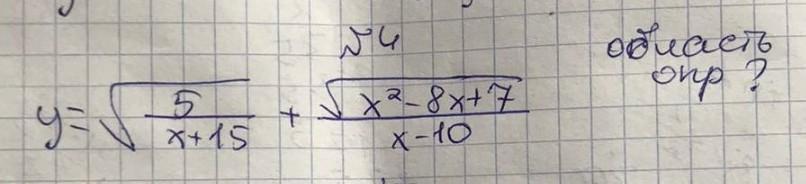Ответы
Ответ дал:
0
Ответ:
составим систему неравенств
изображение решений неравенств во вложениях
по-порядку идут
последнее- общее решение
как начертишь 1 неравенство потом пишешь
x∈ (-15;+∞)
2 решение
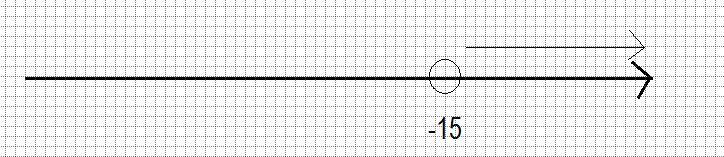
x∈ (-∞;1] ∪ [7; +∞)
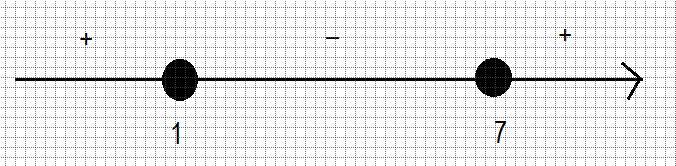
итоговое решение:
x∈ (-15;1] ∪ [7;10) ∪ (10; +∞)
Приложения:
Ответ дал:
2
1) корень
Подкоренное выражение ≥0
Но здесь дробь. Числитель = 5, значит
х+15>0; x>-15
2)-ой корень
х²-8х+7≥0
х²-8х+7=0 парабола, ветви вверх
х1+х2=8; х1*х2=7; х1=7; х2=1 и из знаменателя х≠10
/////////////////////////////////////////////////////////
-------(-15)-----------[1]-----------[7]-------(10)------->x
\\\\\\\\\\\\\\\\\\\\\\\\\ \\\\\\\\\\\ \\\\\\\\\\\\\\\\
Ответ: D(y)=(-15;1]U[7;10)U(10;∞).
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад