Здравствуйте! помогите ,пожалуйста, с логарифмами
Приложения:
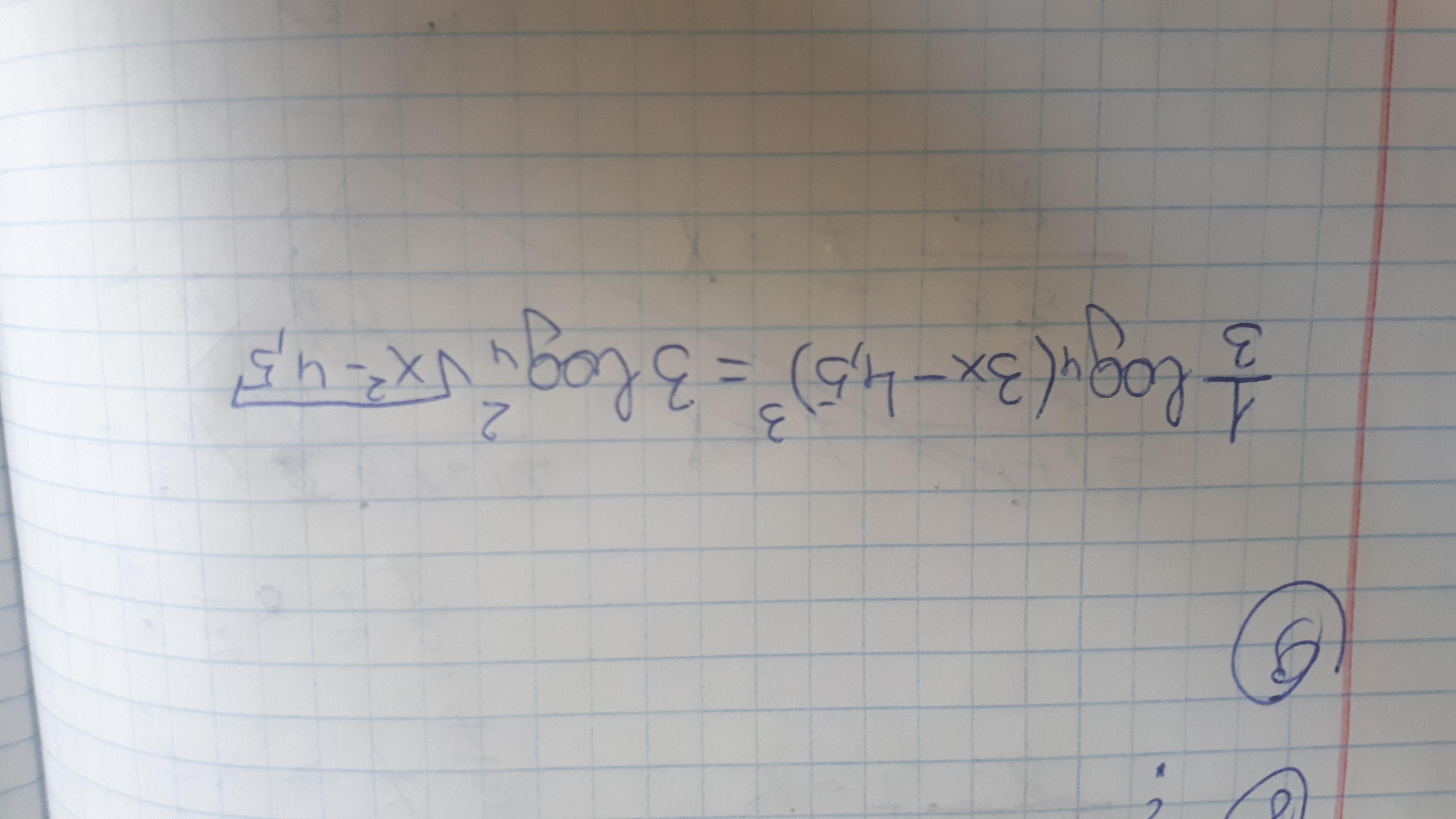
MizoriesKun:
Проверьте условие справа точно вторая степень?? разве не корень третьей степень ?
Да, там стоит вторая степень. Это в егэ20 задание. А со второй никак не решить?
Ответы
Ответ дал:
1
Уравнение решается только в таком виде:
ОДЗ:
⇒
По свойствам логарифма степени: ,
Применяем свойство монотонности логарифмической функции:
каждое свое значение логарифмическая функция принимает ровно в
одной точке.
Поэтому если значения функции равны, то и аргументы равны:
или
не входит в ОДЗ
О т в е т. 3
Я вам очень благодарен! За доступное изъяснение. Но там действительно во второй степени
Бывают и в сборниках опечатки...
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад