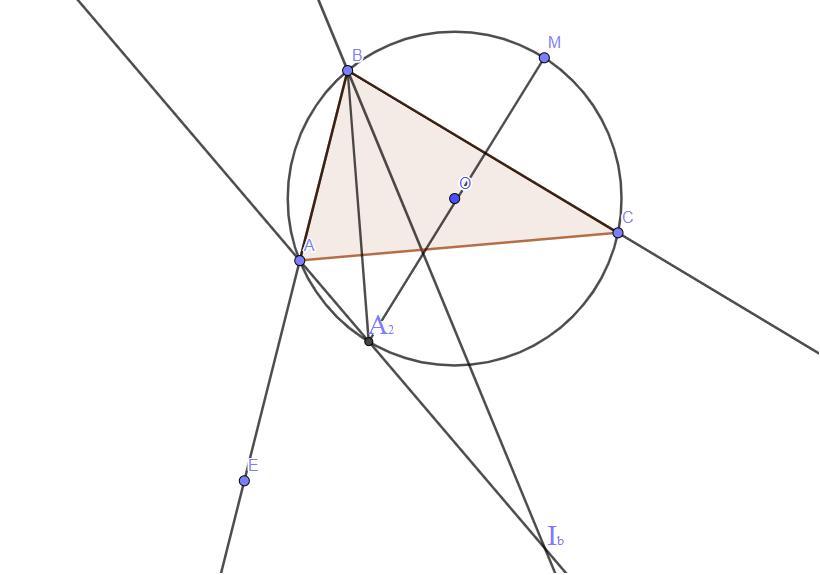
В треугольнике ABC точка Ib — центр вневписанной окружности, касающейся стороны AC, A2 — середина дуги BAC описанной окружности треугольника ABC. Известно, что ∠C=44∘. Найдите углы треугольника BA2Ib.
Ответы
Ответ дал:
5
Пусть . Легко видеть, что
(поскольку
биссектриса угла
). Заметим, что
, так как они опираются на общую дугу
. Более того, треугольник
равнобедренный, поскольку
(
— середина дуги), и
. Имеем:
, откуда
. Итого:
.
Пусть — биссектриса угла
(
— середина дуги
). Тогда
. Более того, поскольку
является биссектрисой внешнего угла
, то
, откуда
. Значит,
лежит на отрезке
.
Здесь уже просто: . Оставшийся угол:
.
Итак, углы треугольника: .
Ответ: .
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад