Ответы
Ответ дал:
1
Ответ:
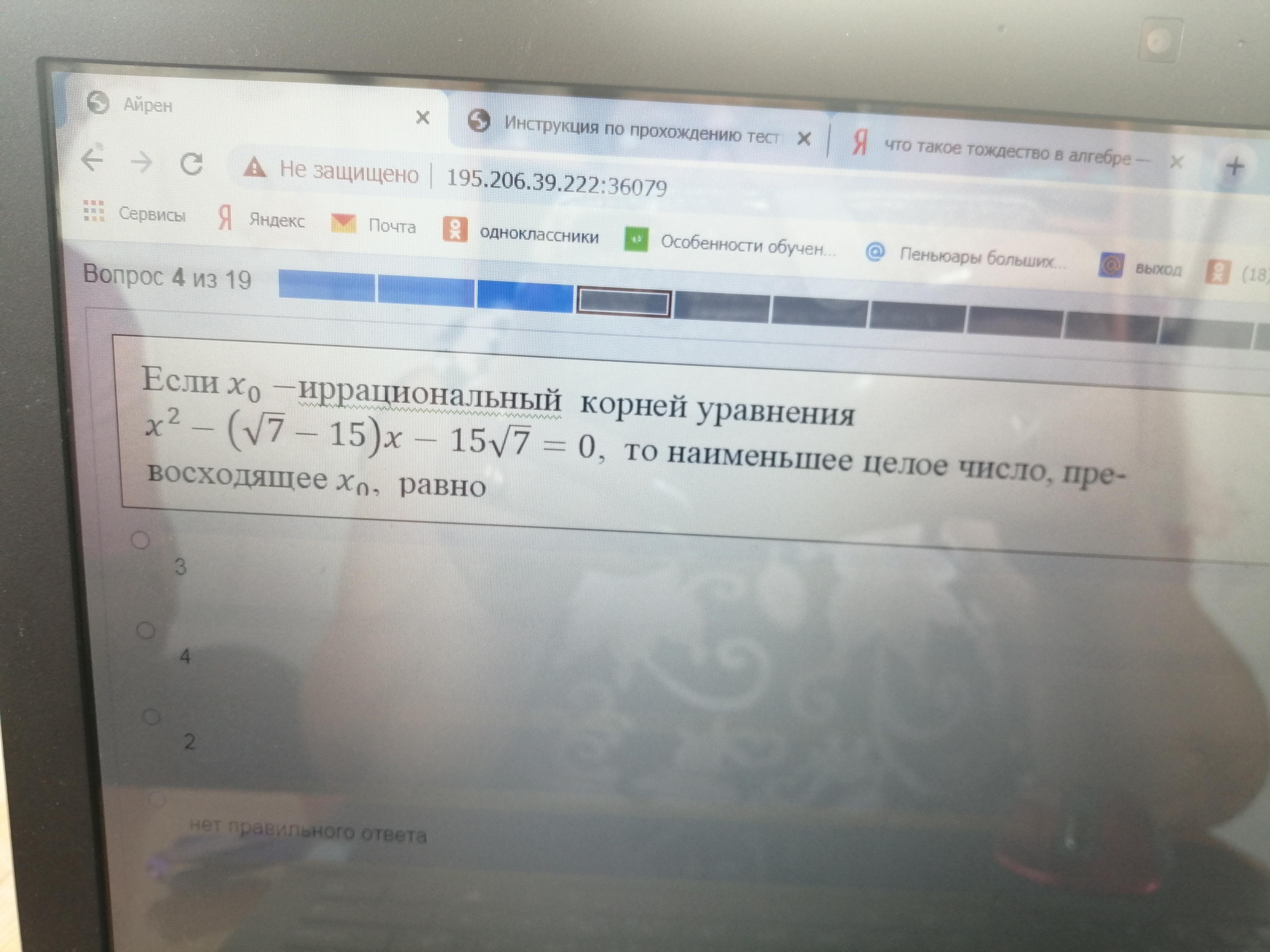
Иррациональным корнем является корень
Наименьшее целое число, превосходящее равно
, так как
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад