Question

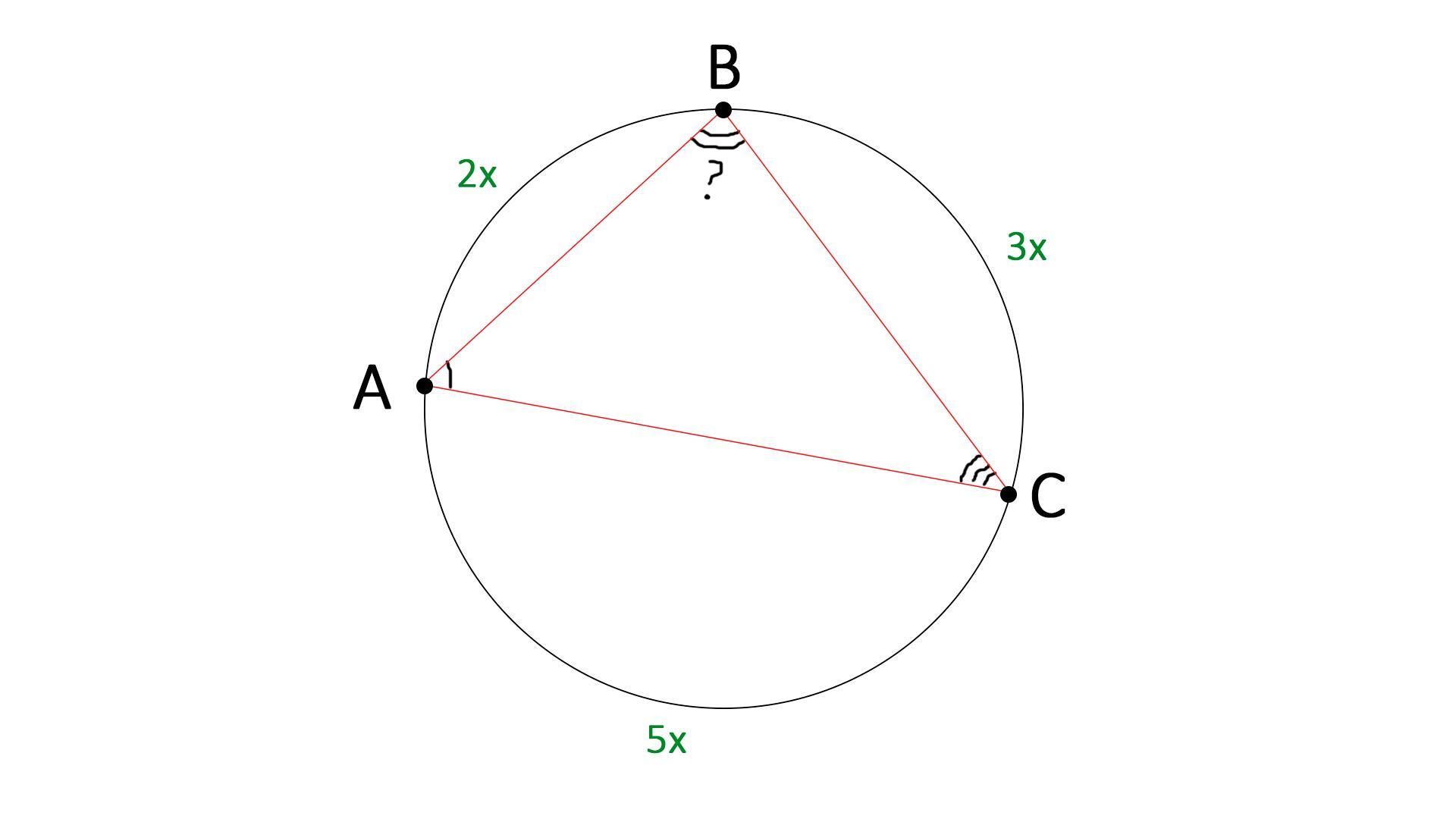
Точки А, В и С, расположенные на окружности, делят её на три дуги. Градусные меры этих дуг относятся как 2 : 3 : 5. Найдите больший угол треугольника АВС. Ответ дайте в градусах.
С решением и рисунком ​

Answer 1

Ответ:

90°

Объяснение:

Вся окружность 360. Точки А,в, С развили ее на части :

от А до В две части  (2к),

от В до С три части (3к),

от С до А пять частей (5к),

2к+3к+5к=360 , к=36 .

Больший угол В,  треугольника АВС,  лежит против большей дуги равной 5*36=180°.

∠В- вписанный. ∠В=1\2*180=90°

Answer 2

ωAB : ωBC : ωAC = 2 : 3 : 5

1)

Пусть дуга AB = 2x, тогда дуга BC = 3x, a дуга АС = 5x, составим уравнение(учитывая что вся окружность = 360°) :

2x+3x+5x = 360

10x = 360

x = 36°

2)

Самая большая дуга AC = 5 * 36 = 180 °

3)

Напротив самой большой дуги лежит самый большой вписанный угол, который = 180 : 2 = 90°

Ответ : 90°