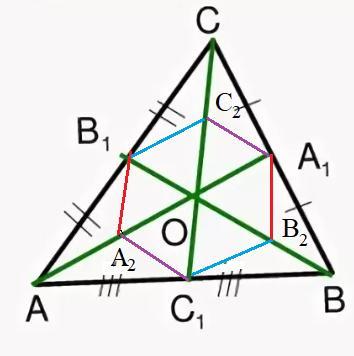
В треугольнике `ABC` его медианы `A A_1`, `B B_1` и `C C_1` пересекаются в точке `O`. Середины отрезков `OA`, `OB` и `OC` обозначены соответственно `A_2`, `B_2` и `C_2`. Выразите периметр шестиугольника `A_2C_1B_2A_1C_2B_1` через медианы `m_a=A A_1`, `m_b=B B_1`, `m_c=C C_1`.
ПОМОГИТЕ ПОЖАЛУЙСТА . ДАЮ 20 БАЛЛОВ. ДАЙТЕ ПОЖАЛУЙСТА ПОЛНОЕ РЕШЕНИЕ
orjabinina:
ответ есть ? Вроде 1/3*( ма+мв+мс)
Ответы
Ответ дал:
10
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
и
- средние линии треугольников АОВ и ВОС
=
=
и
- средние линии треугольников АОС и ВОС
=
=
и
- средние линии треугольников АОВ и АОС
=
=
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад