Найти сумму целых решений или решение неравенства||3(x-4)^2-1|-5<6
orjabinina:
Почему ".....а||3(..........|..........." ?
12, вроде.
Ответы
Ответ дал:
1
Найти сумму целых решений или решение неравенства |3(x-4)^2-1|-5<6
Пошаговое объяснение:
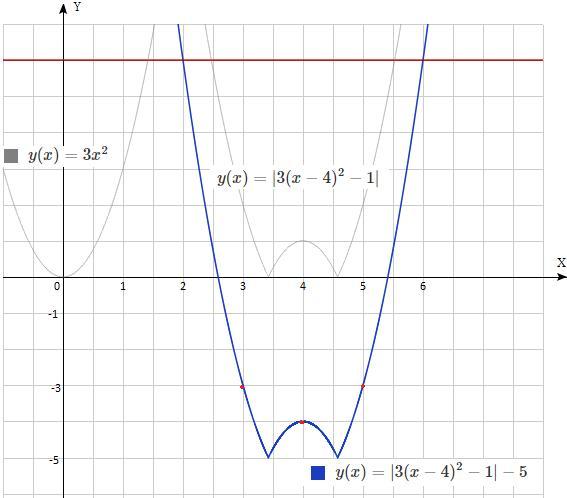
Построим два графика функций у=|3(x-4)²-1|-5 , у=6. Найдем все решения , которые лежат ниже прямой , из них выберем целые.
у=|3(x-4)²-1|-5 можно получить из параболы у=3х² преобразованиями
- сдвиг у=3х² по ох на 4 вправо (у=3(x-4)²) ;
- сдвиг у=3(х-4)²по оу на 1 вниз (у=3(x-4)²-1);
- отображение части параболы относительно оси ох у=|3(x-4)²-1| ;
- сдвиг у=|3(x-4)²-1| на 5 вниз по оу (у=|3(x-4)²-1|-5).
у=6 прямая .
Целыми решениями будут х=3,х=4,х=5. С умма равна 12
Приложения:
можете объяснить на этом примере? https://znanija.com/task/37818478
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад