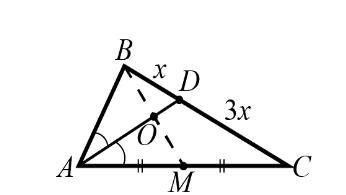
В треугoльнике ABC биcceктриса AD дeлит cтoрoну BC в oтнoшeнии BD:DC=1:3. Мeдиaнa BM пeрeceкaeт бисceктриcу AD в точке O. Найдите oтнoшения BO:OM и AO:OD.
Приложения:
Ответы
Ответ дал:
1
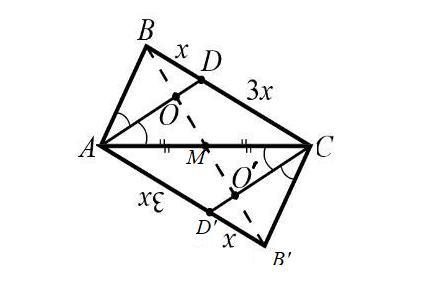
Построим на стороне AC треугольник ACB', равный треугольнику ABC (см. рис.)
Треугольники AOB' и D'O'B', очевидно, подобны. Поэтому . Но
, поэтому
.
Поскольку является биссектрисой, то
, в то же время
. Следовательно,
Приложения:
Ответ дал:
1
Ответ:
=============================
Объяснение:
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад