Question

Найдите наименьшее значение функции

Answer 1

$f(x) = \sqrt{8x-x^2+9} = \sqrt{-(x^2-8x)+9)} = \sqrt{(-x^2 - 8x + 16-16)+9} = \sqrt{-(x^2 - 8x + 16) + 9 +16} = \sqrt{-(x-4)^2 + 25} = \sqrt{25-(x-4)^2}$

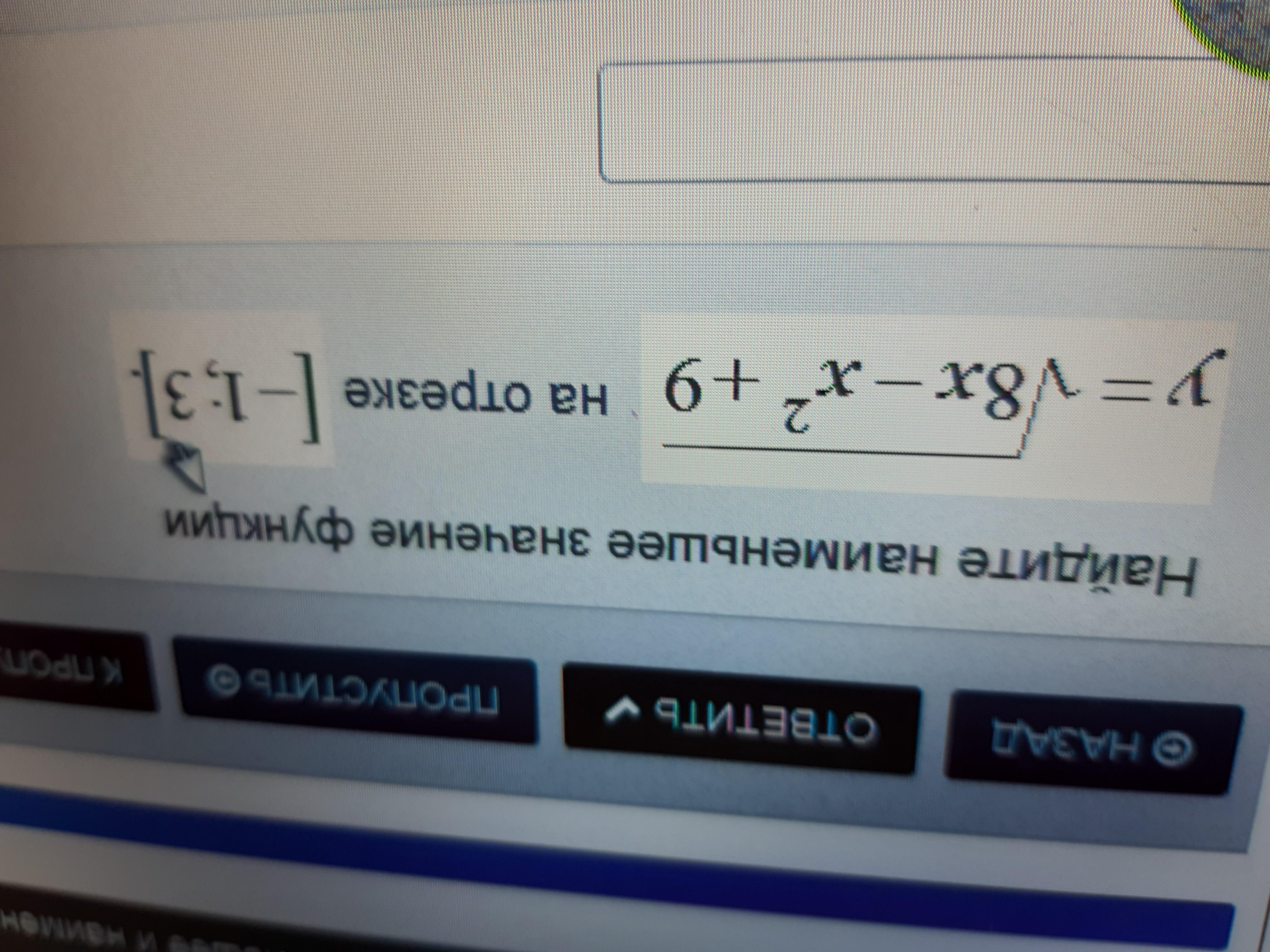
Функция возрастает до x = 4, а после убывает. Значит, минимум соответствует точке x = -1 => $f_{min} = f(-1) = \sqrt{25 - (-1-4)^2} = 0$

Ответ: 0

Answer 2

Ответ:0

Объяснение:

Заметим, что y(-1) = √(-8-1+9) = 0

Поскольку радикал неотрицателен, то 0 его наименьшее значение.