Пожалуйста, помогите с решением задания, срочно нужно! И очень нужен развернутое решения, чтобы понять как решать. Пожалуйста.
Приложения:
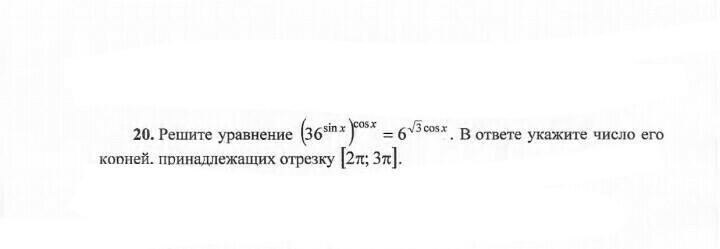
Ответы
Ответ дал:
0
-------------------
-----------------------------
Корни принадлежащие отрезку [2π ; 3π] :
5π/2 ; 7π/3 ; 8π/3
Ответ : 5π/2 ; 7π/3 ; 8π/3
p.s но я не уверен что правильно
Ответ дал:
0
Відповідь:
x=(7pi)/(3)
x=(5pi)/(2)
Пояснення:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад