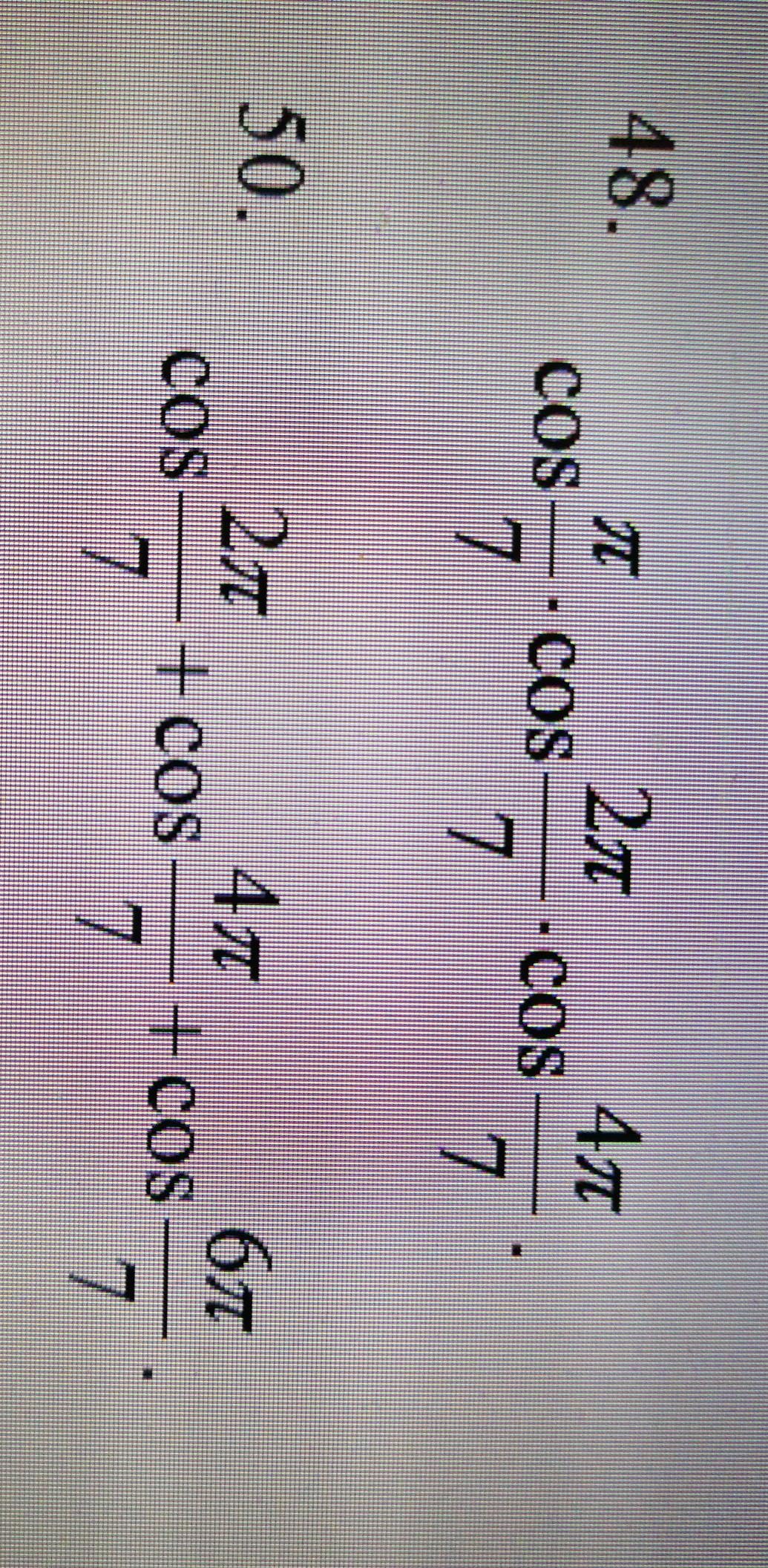Ответы
Ответ дал:
1
Ответ:
Объяснение:
48. Домножим числитель и знаменатель на sin(x)
Ответ:
50. Перепишем исходное выражение, как
Умножим числитель и знаменатель на sin(2x). Получим
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад