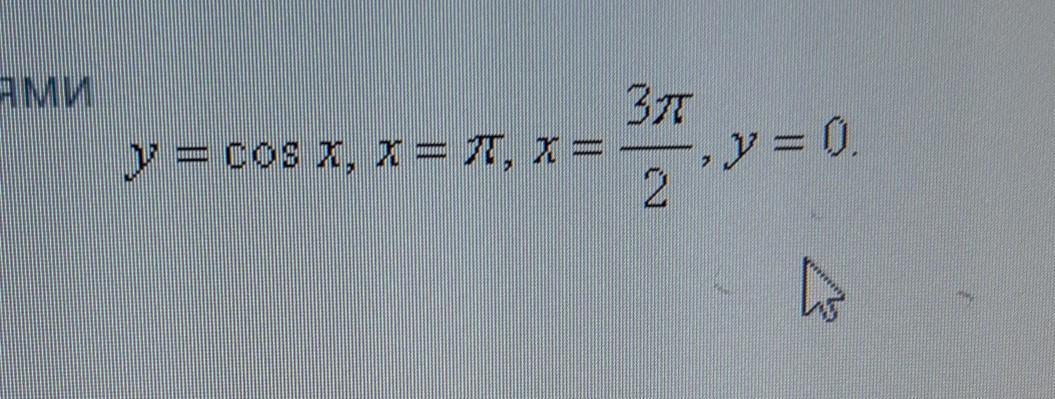Ответы
Ответ дал:
1
Ответ:
Площадь фигуры .
aydarfattahov99:
получается ответ 1
да ?
Да
спасибо
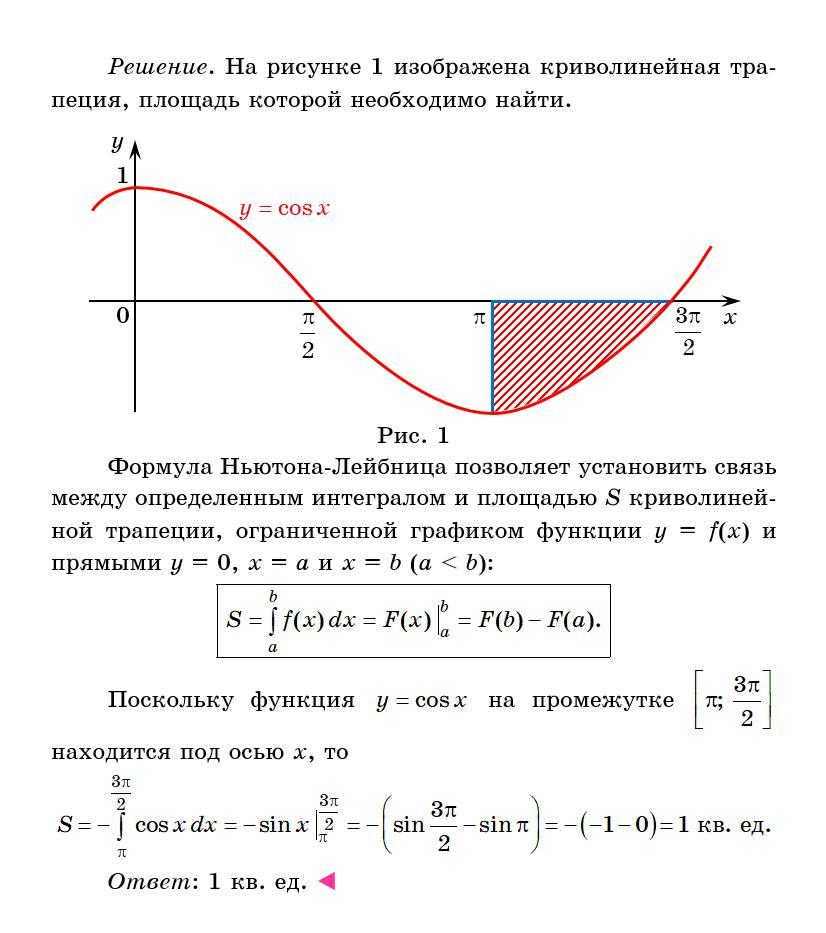
На этом промежутке cos(x) принимает отрицательные значения, поэтому интеграл отрицательный
Но площадь отрицательной быть не может
Поэтому по модулю
А там снизу ответили что ответ 2
Ответ дал:
1
Найдите площадь фигуры, ограниченной линиями ,
,
,
Приложения:
какой ответ то 1 или 2 ?
Перезагрузите страницу
перезагрузил
ответ какой ?
ответ 1
1 кв. ед.
ааа
С каких пор модераторы стали постить плагиат
Это мое личное решение, напечатанное в Microsoft Word.
Ладно спасибо всем вам
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад