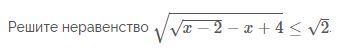Ответы
Ответ дал:
1
ОДЗ :
x - 2 ≥ 0 => x ≥ 2
Рассмотри два случая :
1. x - 4 ≥ 0 => x ≥ 4 :
Возведем обе части уравнения в квадрат :
+ - +
--------------[3]-------------[6]---------------
x ∈ [3 ; 6]
2. x - 4 < 0 => x < 4
x ∈ R
Обьеденение : x ∈ [2 ; 6]
_____________________________________________
, x - 2 ≥ 0 => x ≥ 2
+ - +
--------------[2]--------------[3]---------------
x ∈ (-∞ ; 2] U [3 ; +∞)
Ответ : x ∈ [3 ; 6] U {2}
yanameste:
Помогите пожалуйста https://znanija.com/task/37832719
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад