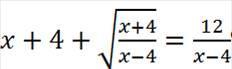Ответы
Ответ дал:
0
Умножаем обе части уравнения на (x-4)≠0:
Замена переменной:
D=49
( не удовл условию t ≥0)
Обратный переход:
При x=5
- верно, так как 9+3=12
При x=-5
- неверно, так как
- неверно
О т в е т. 5
Замена переменной:
⇒
Уравнение принимает вид:
Пропорция, умножаем крайние и средние члены пропорции:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад