Question

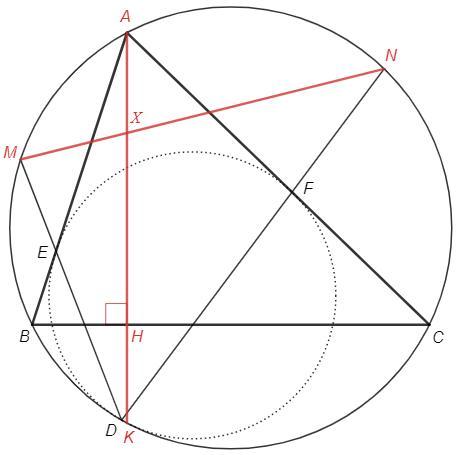
Окружность касается описанной окружности ω треугольника ABC внутренним образом в точке D, а отрезков AB и AC — в точках E и F соответственно. Прямые DE и DF повторно пересекают окружность в точках M и N соответственно. Найдите угол между прямой MN и высотой из вершины A, если ∠B=72∘, ∠C=44∘.

Answer 1

Лемма Архимеда:

Пунктирная окружность вписана в сегмент окружности w, касается окружности w в точке D и хорды AB в точке E. Тогда DE - биссектриса угла ADB.  

По лемме Архимеда M - середина дуги AB, N - середина дуги AC.

∪AN =∪AC/2 =B

∪MB =∪AB/2 =C

∪BK =2BAK =2(90-B) (из треугольника BAH)

X =(∪AN+∪MK)/2 =(C-B)/2 +90 =(44-72)/2 +90 =76°