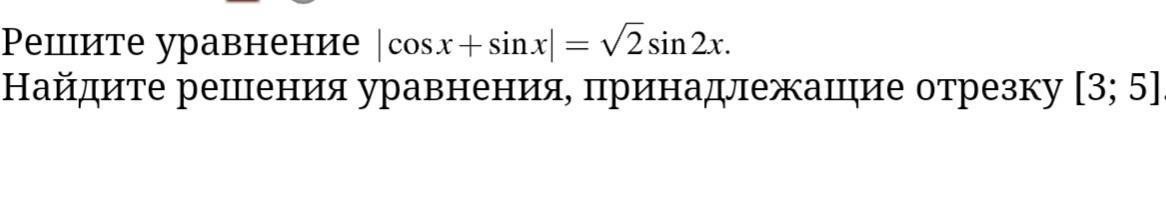Ответы
Ответ дал:
0
......................................................
Приложения:

Ответ дал:
0
Проверяем найденные корни:
Тождество соблюдается, корень подходит.
Тождество не соблюдается, данный корень решением не является.
Тождество не соблюдается, данный корень решением не является.
Общее решение:
Решение, которое принадлежит промежутку:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад