Аналитическая геометрия. Пожалуйста, максимально подробно, с описанием всех действий.
Приложения:
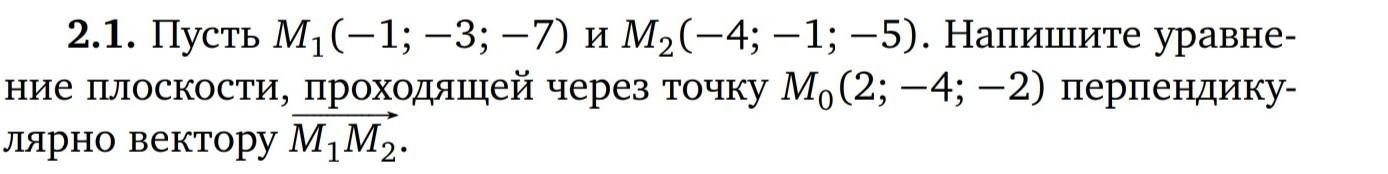
Ответы
Ответ дал:
2
Уравнение плоскости проходящей через точку с координатами перпендикулярно вектору
, имеет вид
Подставляя координаты точки и координаты вектора
, имеем
Уравнение искомой плоскости -3x + 2y + 2z + 18 = 0.
ChiStS:
благодарю
спасибо
Спасибо за подробный ответ.
Ответ дал:
1
Найдем координаты Вектора М₁М₂, вычитая из координат конца, координаты начала. М₁М₂(-4+1;-1+3;-5+7); М₁М₂(-3;2;2)
Уравнение плоскости, проходящей через точку М₀(2;-4;-2) перпендикулярно вектору М₁М₂(-3;2;2) , имеет вид
-3*(х-2)+2*(у+4)+2*(z+2)=0
-3х+2у+2z+6+8+4=0
3х-2у-2z-18=0
Ответ 3х-2у-2z-18=0
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад