Question

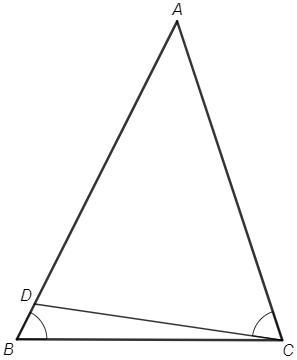
В треугольнике ABC на стороне AB выбрана точка D так, что AD:DB=8:1. Известно, что треугольники ABC И ACD подобны, CD=
$2 \sqrt{10}$
, угол BAC =45. Определить площадь треугольника BCD. ​

Answer 1

S(ABC)/S(ACD) =AB/AD =9/8

ABC~ACD => S(ABC)/S(ACD) =k^2 => k=√(9/8)

AC=AD*k

CD^2 =AC^2 +AD^2 -2AC*AD*cosA =AD^2 (k^2 +1 -2kcosA)

AD^2 =40/(9/8 +1 -3/2) =64

AD=8; AC=6√2

S(ACD) =1/2 AC*AD*sinA =24

S(BCD) =1/8 S(ACD) =3