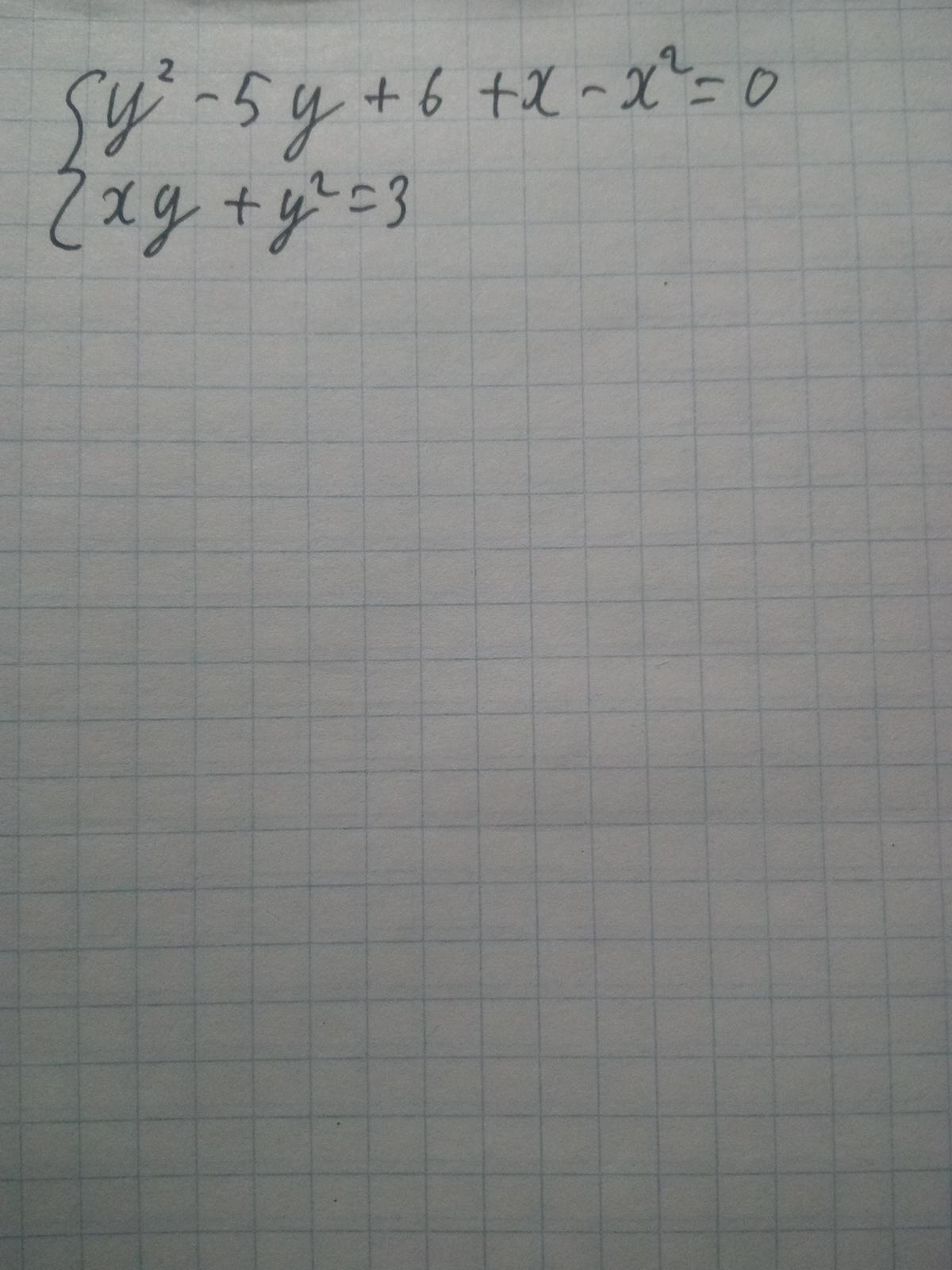Ответы
Ответ дал:
1
Преобразуем первое уравнение системы:
Произведение равно нулю тогда, когда один из множителей равен нулю, а остальные существуют. Здесь ограничений на x и y нет, так что просто приравняем множители к нулю и рассмотрим два случая: первый, когда первый множитель ноль и второй, когда второй множитель ноль.
Первый случай:
1)
Решаем второе уравнение системы:
Теперь найдем соответствующие x:
Второй случай:
Здесь вроде бы все понятно и без комментариев.
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад