Question

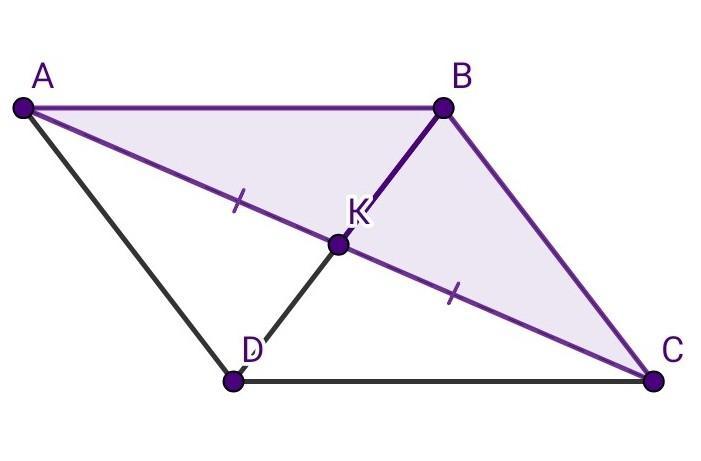
Диагонали AC и BD параллелограмма ABCD пересекаются в точке K. Докажите, что площади треугольников ABK и BCK равны

Answer 1

Дано :

Четырёхугольник ABCD — параллелограмм.

Отрезки BD и АС — диагонали.

Точка К — точка пересечения диагоналей.

Доказать :

S(∆ABK) = S(∆BCK).

Доказательство :

• Диагонали параллелограмма точкой пересечения делятся пополам.

Отсюда АК = СК.

Рассмотрим ∆АВС.

Отрезок ВК — медиана (по определению).

• Медиана треугольника делит треугольник на два равновеликих (равных по площади) треугольника.

Отсюда S(∆ABK) = S(∆BCK).

Ответ :

Что требовалось доказать.