Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Ответы
Ответ:
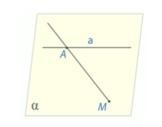
Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам
нужно доказать, что все прямые, которые проходят через точку М и пересекают
прямую а лежат в некоторой единственной плоскости.
Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит
единственная плоскость, обозначим через. Теперь возьмем произвольную
прямую, которая проходит через точку М и пересекает прямую а, например, в
точке А. Прямая МА лежит в плоскости α, потому что две ее точки М и А, лежат в
этой плоскости. Значит, и вся прямая лежит в плоскости, в силу 2 аксиомы.
Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи,
и доказали, что она лежит в плоскости α. Значит, все прямые, проходящие через
точку М и пересекающие прямую а лежат в плоскости α, что и требовалось
доказать
Объяснение: