Для правильного шестиугольника
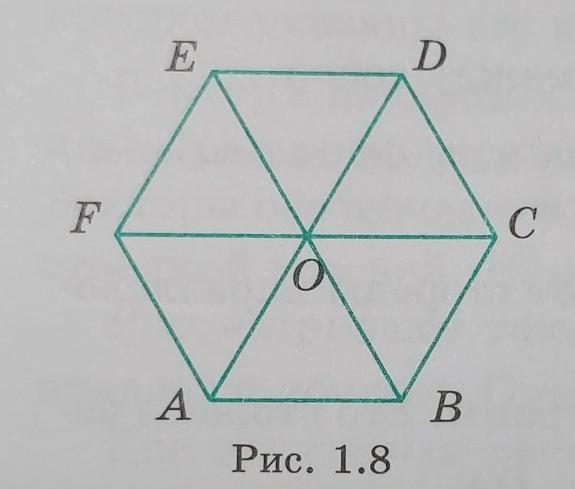
ABCDEF и точки О пересечения его диагоналей (рис. 1.8) запишите векторы с началом и концом в вершинах этого шестиугольника, равные вектору:
а) АО; б) Ос.
Приложения:
Ответы
Ответ дал:
26
В правильном шестиугольнике все стороны равны, а сторона равна радиусу.
Равные векторы - это векторы, у которых равны длины и одинаковое направление.
Поэтому:
а) АО = FE = BC;
б) ОС = АВ = ED.
Ответ дал:
31
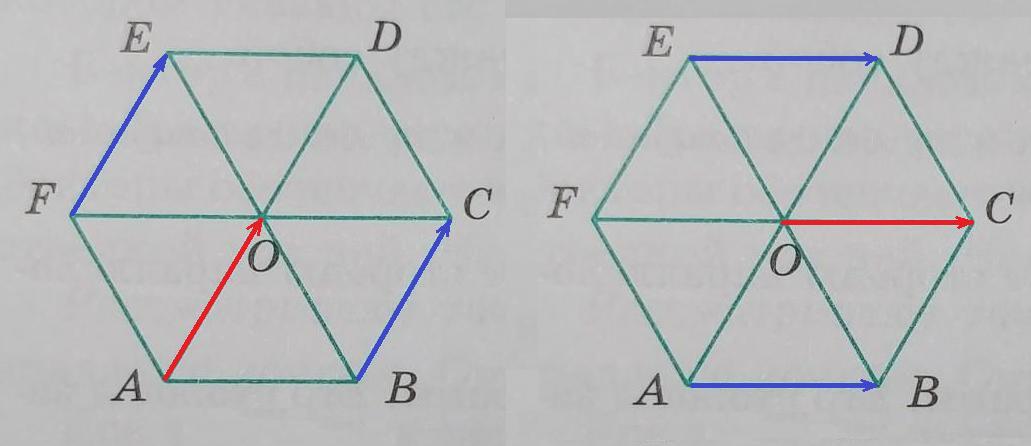
Равные векторы имеют одинаковую длину, совпадающие направления и лежат на параллельных прямых или одной прямой (на каждом рисунке все указанные векторы с началом и концом в вершинах шестиугольника направлены в одну сторону, лежат на параллельных прямых и по длине равны стороне шестиугольника).
а)
б)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад