Question

основания равнобедренного треугольника равна 3, тангенс угла при основании равен 2, найти длину боковой стороны

Answer 1

Ответ:

$\frac{\sqrt{5}*3 }{2}$

Объяснение:

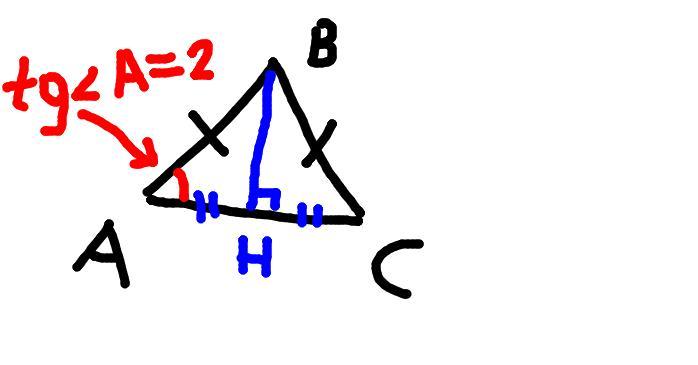
Треугольник ABC (на рис.) равнобедренный с основанием AC.

Проведем высоту BH из угла <B. По свойству высоты равнобедренного треугольника, проведенной к основанию, BH также является медианой.

Значит, AH = CH = 3/2

По условию, tg <A = 2

tg <A = BH/AH ( по определению тангенса угла)

BH = tg <A * AH = 2* (3/2) = 3

По теореме Пифагора ( для треугольника ABH):

AB = $\sqrt{AH^2 + BH^2}$ = $\sqrt{(3/2)^2 + 3^2}$ = $\frac{\sqrt{5}*3 }{2}$ - длина боковой стороны