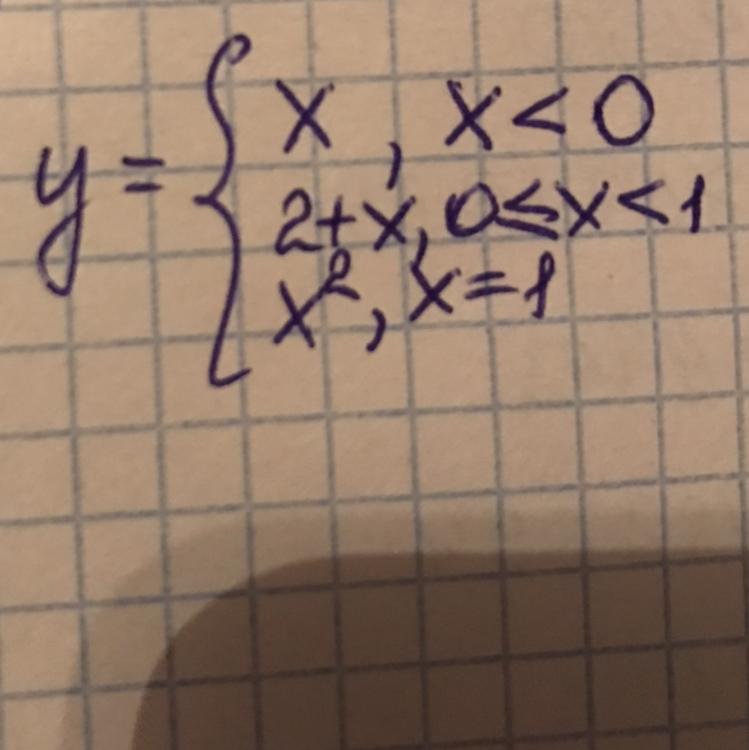Ответы
Ответ дал:
0
Ответ:
Функция является разрывной, т.е. не является непрерывной в точках x=0, x=1.
Пошаговое объяснение:
Приложения:
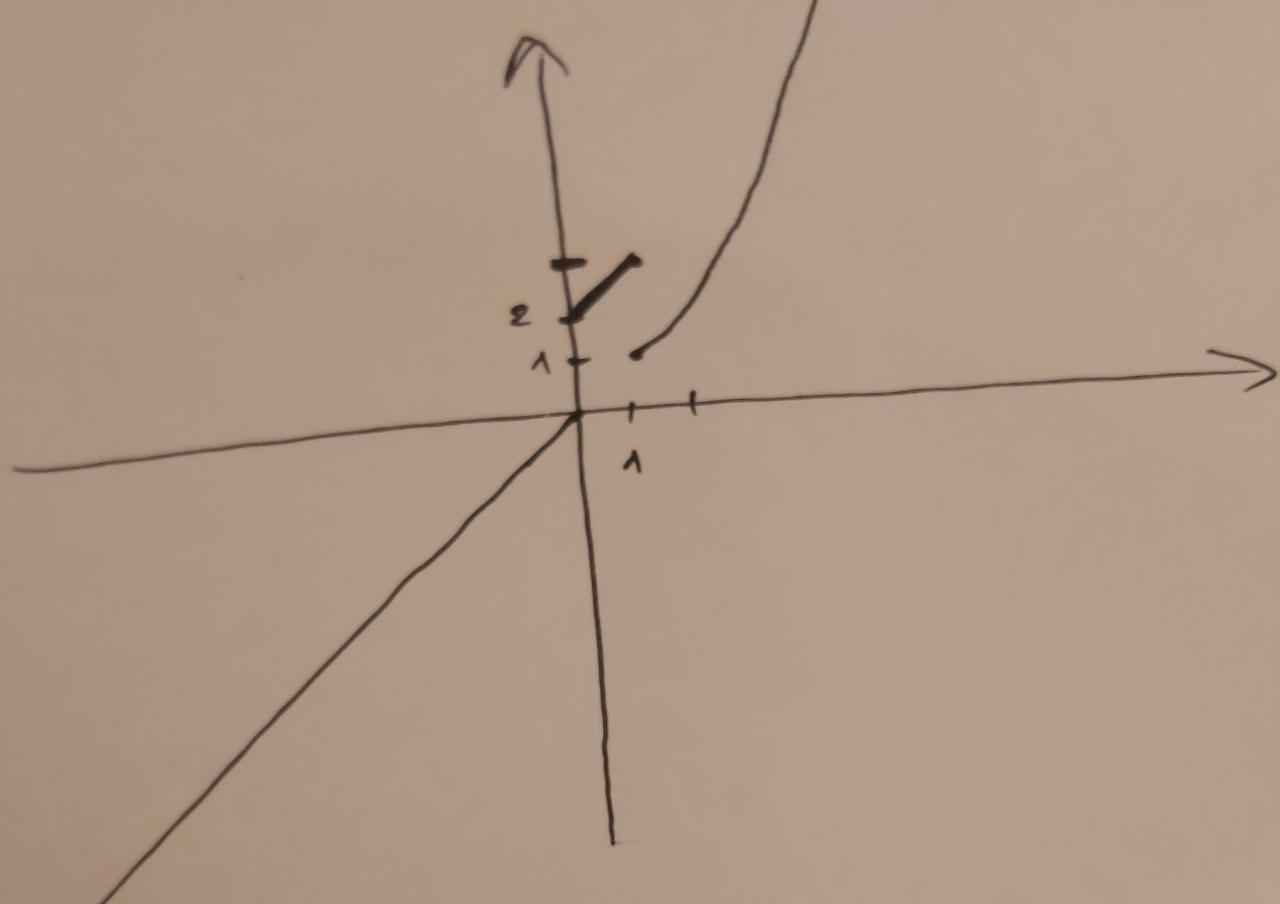
Если х больше единицы, то строим график функции y=x^2 для всех х > 1
Функция f(x) называется непрерывной в точке α, если:
функция f(x) определена в точке α и ее окрестности;
существует конечный предел функции f(x) в точке α;
это предел равен значению функции в точке α
функция f(x) определена в точке α и ее окрестности;
существует конечный предел функции f(x) в точке α;
это предел равен значению функции в точке α
Если функция не является непрерывной, то она является "прерывной" - т.е. разрывной, имеет разрыв.
limf(x) = 0 для x-> 0 - 0 (читается как икс стремится к нулю слева)
lim f (x) = 2 при x - > 2 + 0 (при икс стремящимся к 2 справа)
Левый предел(первый) и правый предел(второй) различный.
Если функция непрерывна в точке, то она имеет предел слева и справа и они должны совпадать.
У нас не совпадает, следовательно, функция не является непрерывной в точке х=0, т.е. разрывна в этой точке.
Если функция непрерывна в точке, то она имеет предел слева и справа и они должны совпадать.
У нас не совпадает, следовательно, функция не является непрерывной в точке х=0, т.е. разрывна в этой точке.
Аналогичные рассуждения для точки х=1.
Хорошо
Спасибо
lim f(x) = 3 при x -> 1 - 0
lim f(x) = 1 при x -> 1 + 0
Пределы слева и справа разные, следовательно в x=1 функция разрывна.
lim f(x) = 1 при x -> 1 + 0
Пределы слева и справа разные, следовательно в x=1 функция разрывна.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад