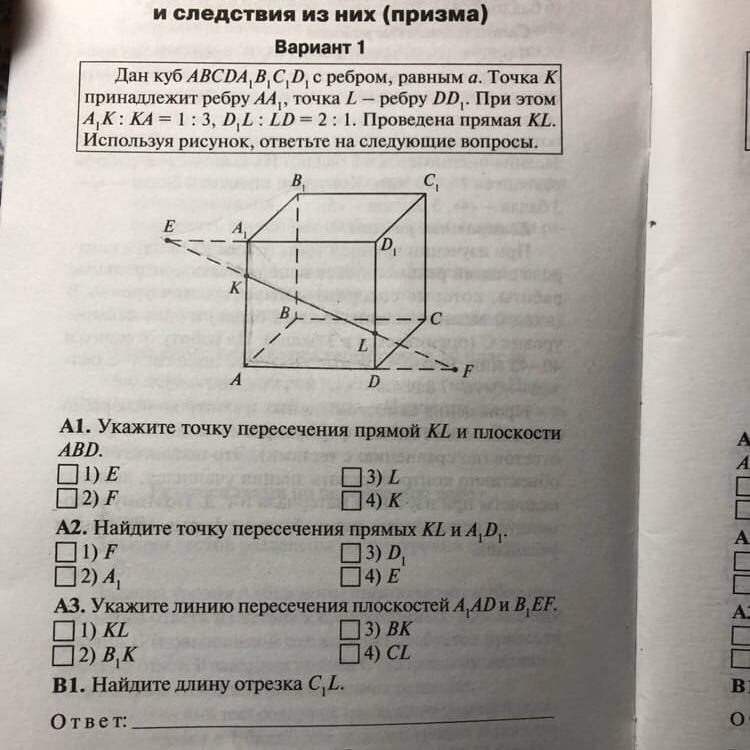
Найдите длину отрезка EF, присутствует рисунок и дано.
Приложения:
orjabinina:
какая то странная задача.Разве может прямая KL в разном отношении пересекать стороны куба?
Честно не знаю.. я не могу понять эту задачу, а ее надо решить очень срочно..
могу написать решение
Да пожалуйста, не могли бы вы решить по подобию треугольников?
не уверена в вычислениях
Ответ должен был быть 13а/5
все исправила
Спасибо огромное
У симбы 2017 решение короче.
Ответы
Ответ дал:
1
Объяснение:
1) ЕF= EК+KL+LF КА= , LD=
, D₁L=
, A₁K=
.
2) Пусть LM⊥AK → КМ=КА-МА= -
=
.
ΔKML-прямоугольный , по т. Пифагора КL=√(а²+ ( )²)=
√169=
.
3) ΔЕLD₁-подобен Δ ЕКА₁ ( п 2 углам -общий и прямой) : ,
8ЕК=3ЕК+3КL , 5ЕК=3КL , ЕК=*
=
4) ΔFKA-подобен ΔFLD ( п 2 углам -общий и прямой) :
,
9FL=4FL+4LK ,5FL=4LK , FL=4/5*KL= .
5) ЕF= EК+KL+LF = +
+
=
.
Приложения:
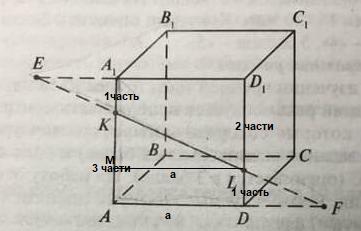
А почему мы проводим прямую ещё дополнительную? Можете пожалуйста объяснить
чтбы найти КL
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад