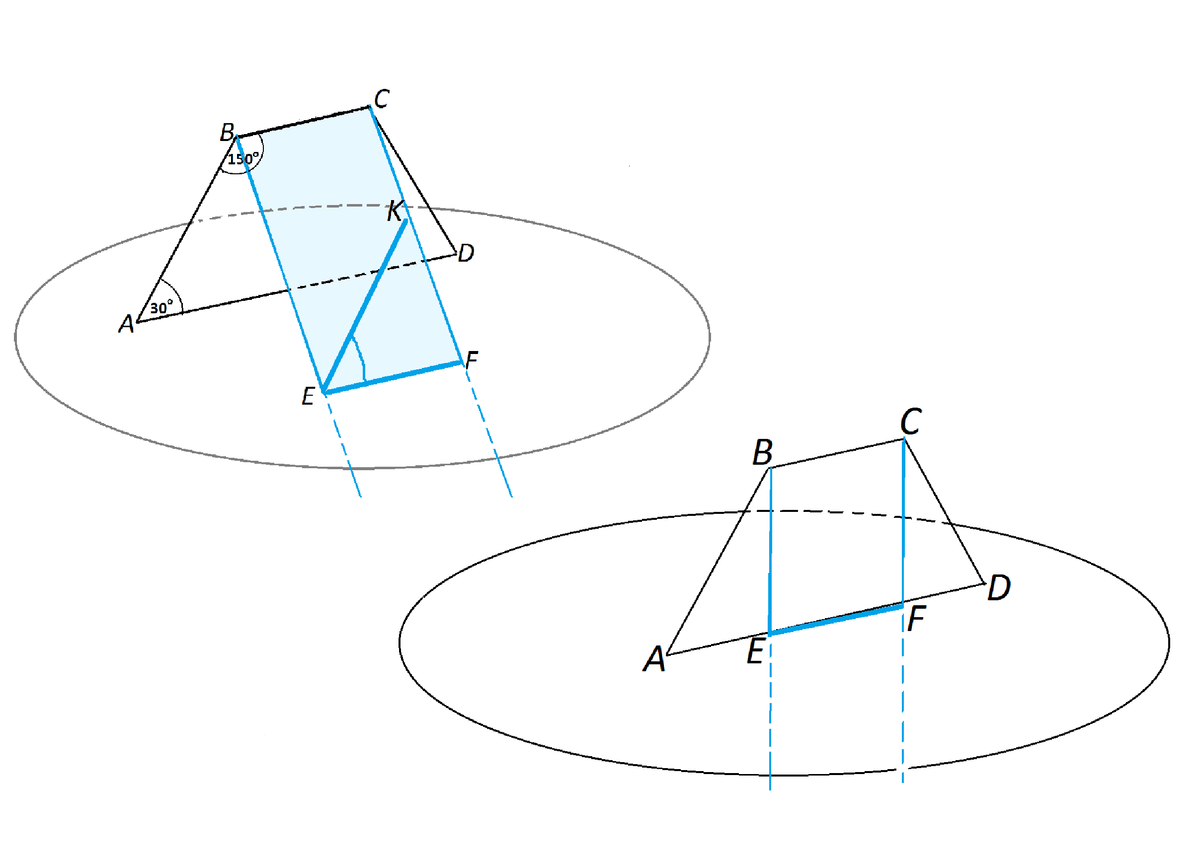
Основание АD трапеции ABCD лежит в плоскости а .Через точки B и C проведены параллельные прямые , пересекающие плоскость а в точках E и F соответственно.
A) Каково взаимное положение прямых EF и AB ?
Б)Чему равен угол между прямыми EF и АB,если угол ABC= 150 градусам ? Поясните .
Пожалуйста дайте ответ подробнее .
Туго с Геометрией ;(
Ответы
1) Каково взаимное расположение прямых EF и AB?
(Уточняем - в плоскости α лежит только АД, а ВС - не лежит. В противном случае ВЕ и СF не пересекали бы плоскость α, а лежали в ней).
ВС параллельна АD ⇒ параллельна плоскости α.
АD параллельна ВС, ЕF параллельна ВС. Две прямые , параллельные третьей прямой, параллельны.
⇒ ЕF параллельна АD и параллельна плоскости АВСD, но не параллельна АВ, которая пересекается с АD.
⇒ Прямые EF и AB - скрещивающиеся.
2) Чему равен угол между прямыми EF и AB, если ABC = 150°?
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Сумма углов при боковой стороне трапеции 180°, следовательно, угол ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
-----------
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.