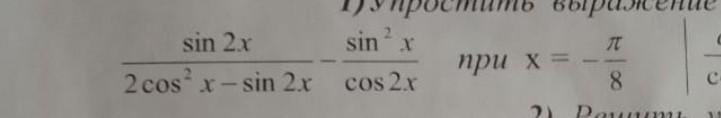Ответы
Ответ дал:
0
sin2x/(2cos^2(x)-2sinx•cosx)= 2sinx•cosx/ 2cosx(cosx-sinx)= sinx/(cosx-sinx)
Sinx/(cosx-sinx) - sin^2(x)/(cosx-sinx)(cosx+sinx) = sinx(cosx+sinx)/cos2x - sin^2(x)/ cos2x = (sinx• cosx + sin^2x- sin^2x)/cos2x= sinx•cosx/cos2x =sin2x/2cos2x
X=-П/8
Sin2x/ 2 cos2x = sin (-П/4)/ 2cos(-П/4)= -1/2
Sinx/(cosx-sinx) - sin^2(x)/(cosx-sinx)(cosx+sinx) = sinx(cosx+sinx)/cos2x - sin^2(x)/ cos2x = (sinx• cosx + sin^2x- sin^2x)/cos2x= sinx•cosx/cos2x =sin2x/2cos2x
X=-П/8
Sin2x/ 2 cos2x = sin (-П/4)/ 2cos(-П/4)= -1/2
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад