Допоможіть будь ласка вирішити даю дуже багато балів
Приложения:
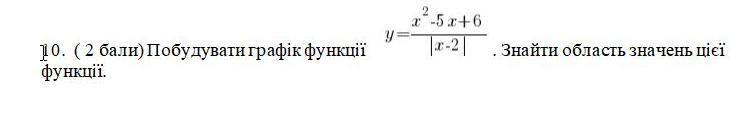
orjabinina:
переведите первые 3 слова
Построить график функции
и найти ОДЗ ?
найти область значений
данной функции
поможешь пожалуста?
lf
Ответы
Ответ дал:
1
............................
обл.значень:(-1;1)∪(1;∞)
Приложения:
Ответ дал:
0
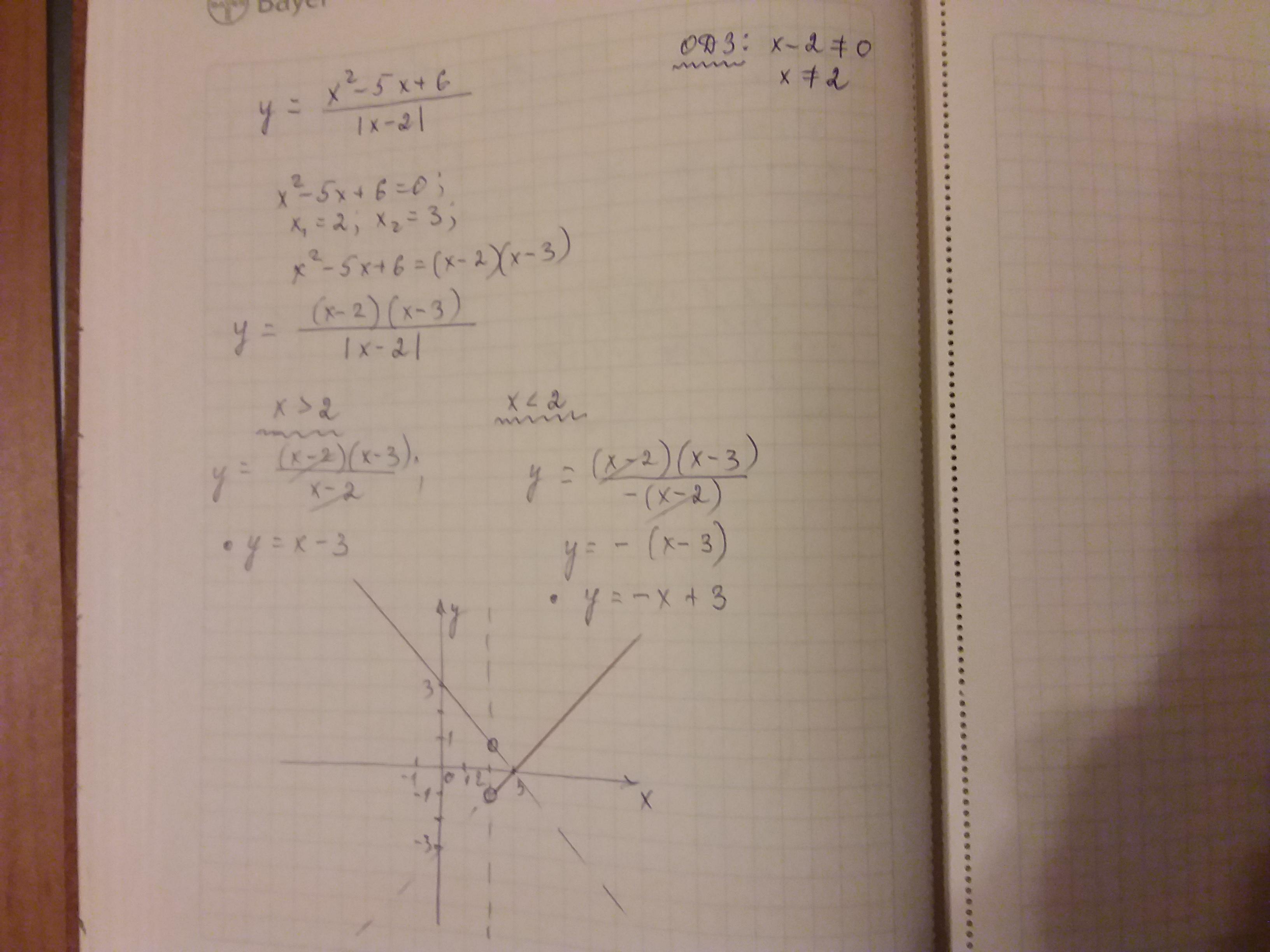
Построить график функции у= . Найти область определения функции
Пошаговое объяснение:
у= . Разложим х²-5х+6 на множители. х²-5х+6=0 ,х=2,х=3
у=
1 случай) Пусть х-2>0, х>2 , тогда |x-2|=x-2
у= . Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
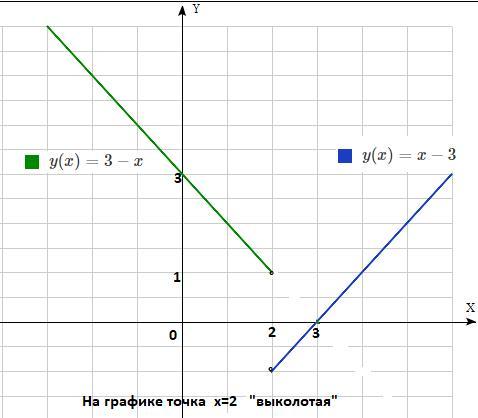
у=х-3 , х≠2. Графиком является прямая
х -2 3
у -5 0
2 случай) Пусть х-2≤0, х≤2 , тогда |x-2|= -(x-2)
у= . Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
у=-(х-3) , у=3-х , х≠2. Графиком является прямая
х -2 3
у 5 0
На графике точка х=2 "выколотая"
Область значений функции (-1 ; 1)∪( 1 ;+∞)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад