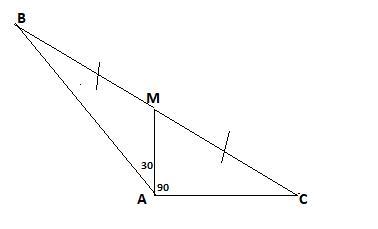
Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30° и 90°.
Simba2017:
ответов в базе много, но нормальных мало
посмотрите https://znanija.com/task/37744201
спасибо
там используется свойство медианы, что она делит треугольник на 2-равные по площади
задача устная , решается без площадей и синусов
Ответы
Ответ дал:
2
Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30° и 90°.
Объяснение:
ΔАВС, АМ-медиана, значит ВМ=МС=х. Найдем .
Для ΔАВМ по т. синусов .
Для ΔАСМ по т. синусов .
Разделим почленно первое уравнение на второе :
.
,
,
. Т.к. sin∠BMA=sin(180-∠CMA)=sin∠CMA, то
.
Приложения:
39 откуда?
Спасибо.
здравствуйте! Помогите с алгеброй, пожалуйста. (в моем профиле) Очень нужно(
Ответ дал:
13
Ответ:
1 : 2
Объяснение:
Приложения:

лаконично)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад