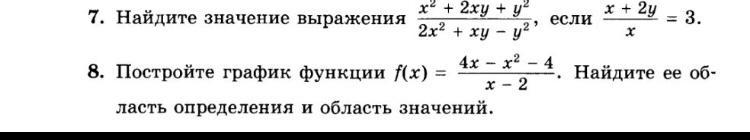Ответы
Ответ дал:
0
Ответ:
1) 2
2)
Обл. определения - все действ. числа кроме 0;
Обл. значений - все действ. числа кроме 2
см. рисунок.
Объяснение:
Известно, что
х ≠0; у ≠ 0
На всякий привожу здесь обратное перемножение разложенных на множители числителя и знаменателя начальной дроби
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад