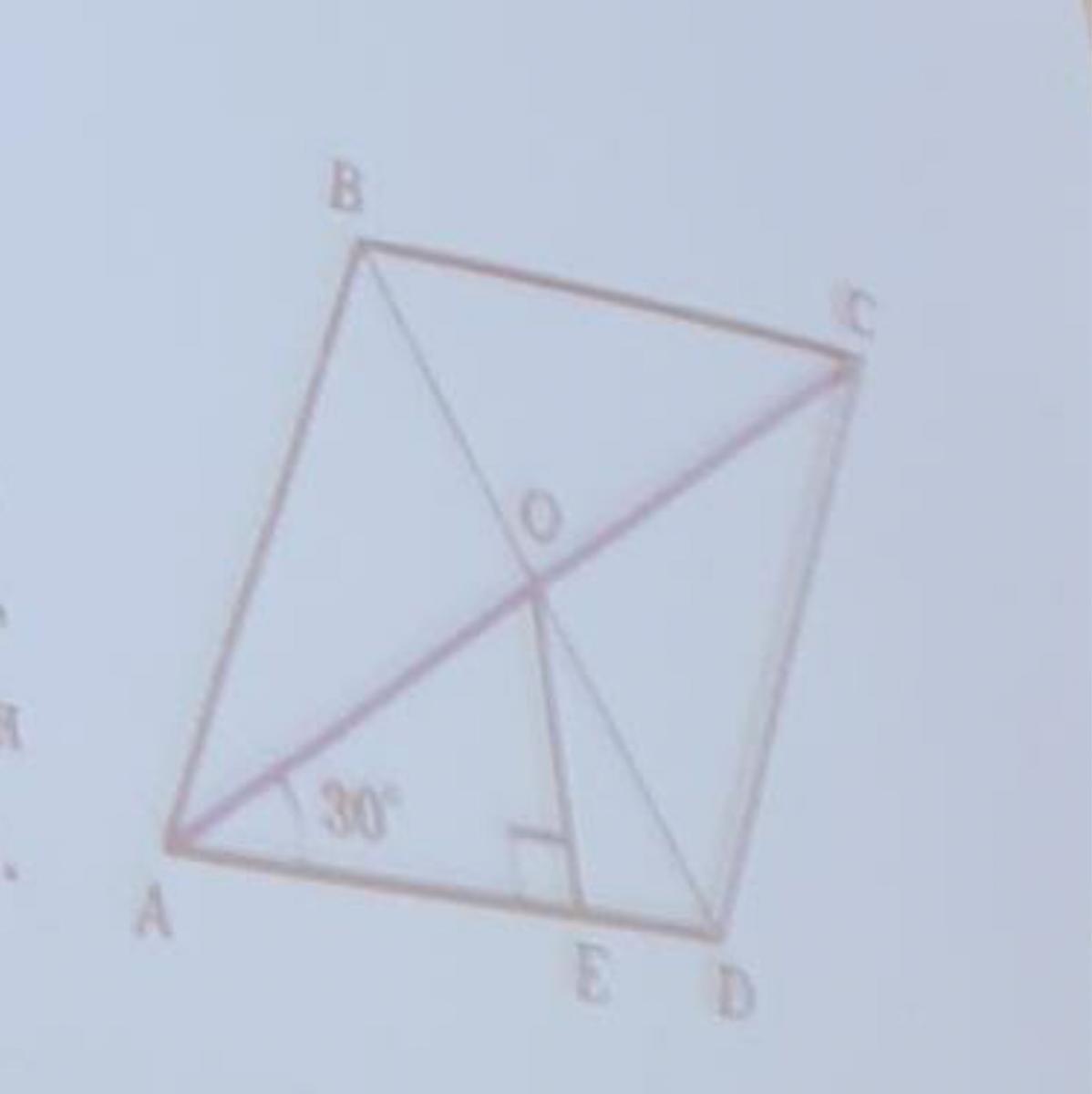
В параллелограмме АBCD диагональ АС, равна 24 см, образует со стороной АD угол в 30°, О—точка
пересечения диагонали АС и BD, ОЕ | AD. Найдите длину отрезка ОЕ.
Р е ш е н и е
Диагонали параллелограмма точкой пересечения____поэтому АО=___=____см. Треугольник АОЕ—прямоугольный с гипотенузой_____и острым углом А, равным_____°. Поэтому катет ОЕ, лежащий против ушла в ___°, равен ___, т.е. ОЕ=____см=____см.
Ответ: ___см.
Приложения:
Ответы
Ответ дал:
9
Ответ:
Решение:
диагонали параллелограмма точкой пересечения делиться пополам (24÷2) и при этом равны, поэтому АО=ОС=12 см. Треугольник АОЕ - прямоугольный с гипотенузой АО и острым углом А, равным 30°. Поэтому катет ОЕ, лежащий против угла в 30°, равен (12÷2) 6, т.е ОЕ=АО=6 см.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад