Ответы
Ответ дал:
3
Ответ:
Объяснение:
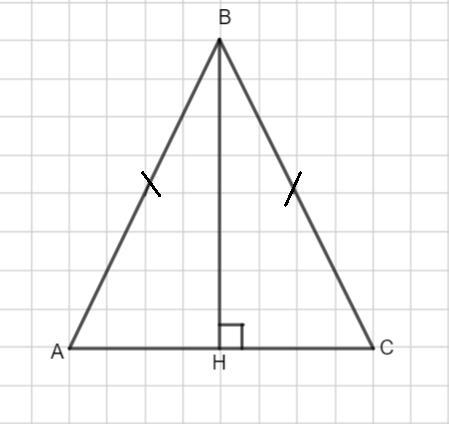
Треугольник АВС - равнобедренный, так как АВ=ВС=10 ед.
Основание АС= 16 ед.
Проведем высоту ВН. В равнобедренном треугольнике высота, проведенная к основанию является медианой.
Значит, АН=НС=16:2=8 ед.
Рассмотрим треугольник АНВ - прямоугольный. Найдем tgA.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Найдем катет ВН из данного прямоугольного треугольника по теореме Пифагора.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад