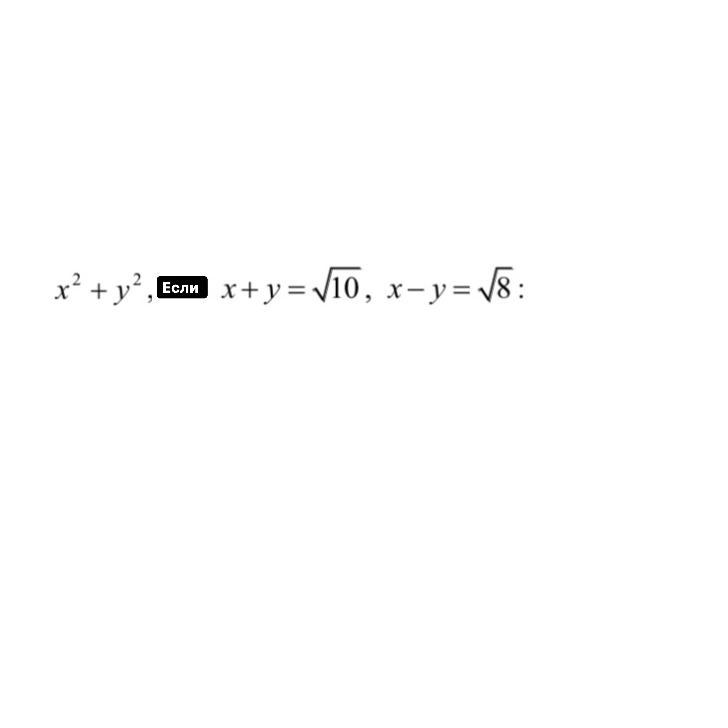Ответы
Ответ дал:
1
Ответ:
9
Объяснение:
Найдём сначала х и у.
Тогда
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад