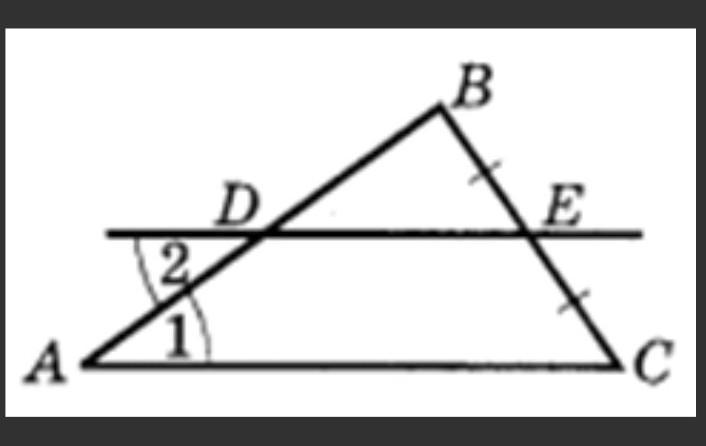
Дан треугольник АВС, причем точка Е – середина стороны ВС, а угол 1 = углу 2. Докажите, что AD=DВ.
Приложения:
Ответы
Ответ дал:
29
Доказательство:
Так как - середина
, значит
.
, по условию ⇒ по признаку параллельности прямых,
.
Значит - средняя линия.
А по свойству средней линии, , то есть
- середина
.
Что и требовалось доказать!
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад