Упростить выражение под буквой а.
Приложения:
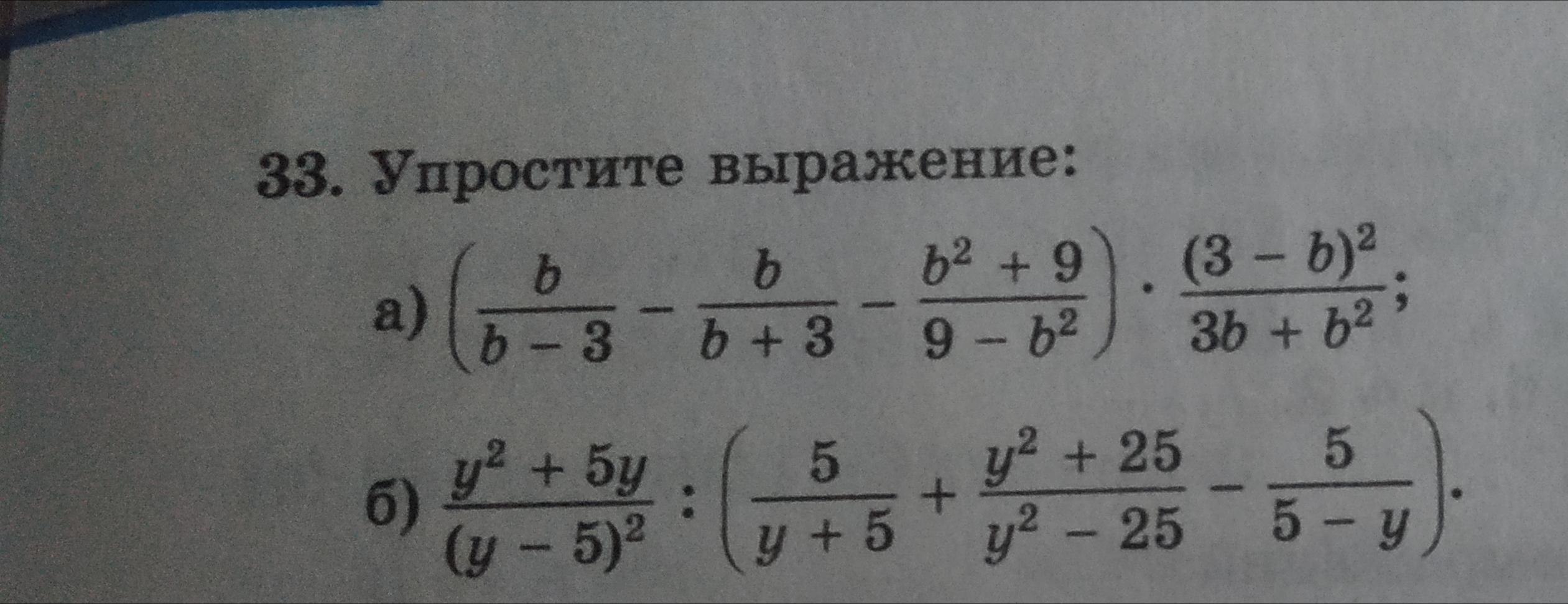
Ra4ok111:
Не давайте ответы если не знаете, если вы напишете бесполезный ответ ради баллов вам выдадут бан
А и не надейтесь баллы получить за бесполезный ответ. Ответ удалят а баллы заберут
Ответы
Ответ дал:
2
а)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад