Ответы
Ответ дал:
3
Объяснение:
x * x + 3x - 4 имеет 2 корня: 1 и -4
Тогда приведем к общему знаменателю всё: (x-1) * (x + 4)
((x + 1) * (x + 1) * (x + 4) - 20 + (x + 1) * (x - 1)) / ((x - 1) * (x + 4)) = x + 1
умножим на (x - 1) * (x + 4)
((x + 1) * (x + 1) * (x + 4) - 20 + (x + 1) * (x - 1)) = (x + 1) * (x - 1) * (x + 4)
раскроем скобки:
x^3 + 6x^2+9x+4 - 20 + x^2 - 1 = x^3+4x^2-x-4
3x^2+10x-13 = 0
D = 10 * 10 + 4 * 13 * 3 = 100 + 12 * 13 = 100 + 156 = 256 = 16 * 16
x1, x2 = (-10 +- 16) / (2 * 3) = (-10 +- 16) / 6 = 1; -(4 + 1/3) можно записать как:
Ответ:
1 и -26/6
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад
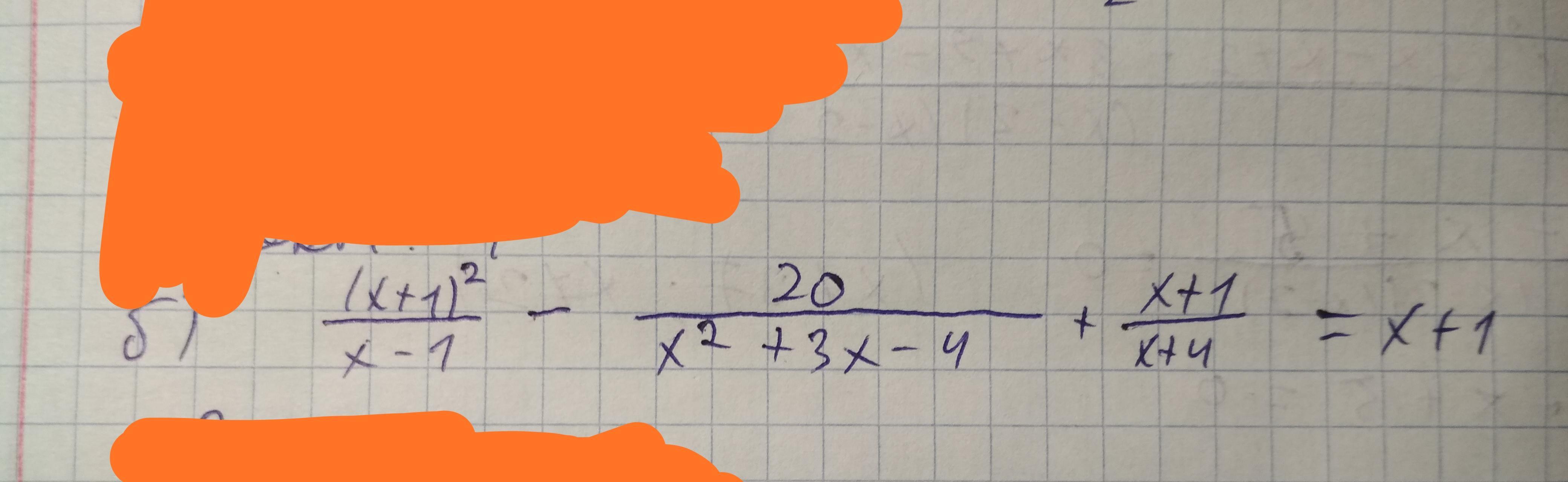
Andrey04dmit@gmail.com
или Telegram:
@drewisme
о себе:
я студент мгу, шарю в матеше