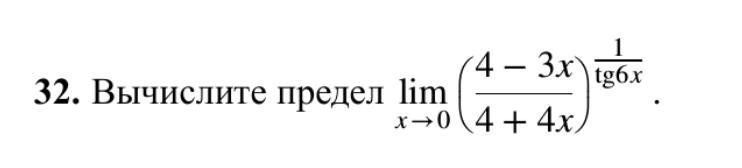Question

Решите задание по матанализу

Answer 1

Ответ: e^(-7/24).

Объяснение:

Подстановка значения x=0 приводит к неопределённости вида 1^∞. Обозначим искомый предел через A и рассмотрим число B=ln(A)=ln lim{1/[tg(6*x)]*ln[(4-3*x)/(4+4*x)]}. По непрерывности логарифмической функции знаки предела и логарифма можно поменять местами, и тогда B=lim{ln 1/[tg(6*x)]*ln[(4-3*x)/(4+4*x)]=lim 1/tg(6*x)*lim ln(4-3*x)/(4+4*x). Но так как при x⇒0 бесконечно малая величина tg(6*x) эквивалентна бесконечно малой 6*x, а бесконечно малая величина ln(4-3*x)/(4+4*x) эквивалентна бесконечно малой (4-3*x)/(4+4*x)-1=-7*x/(4+4*x). Поэтому, заменив исходные бесконечно малые на указанные, перепишем предел в виде B=lim 1/(6*x)*(-7*x)/(4+4*x)=-7/(24+24*x)=-7/24. Но так как B=ln(A), то отсюда A=e^B=e^(-7/24).