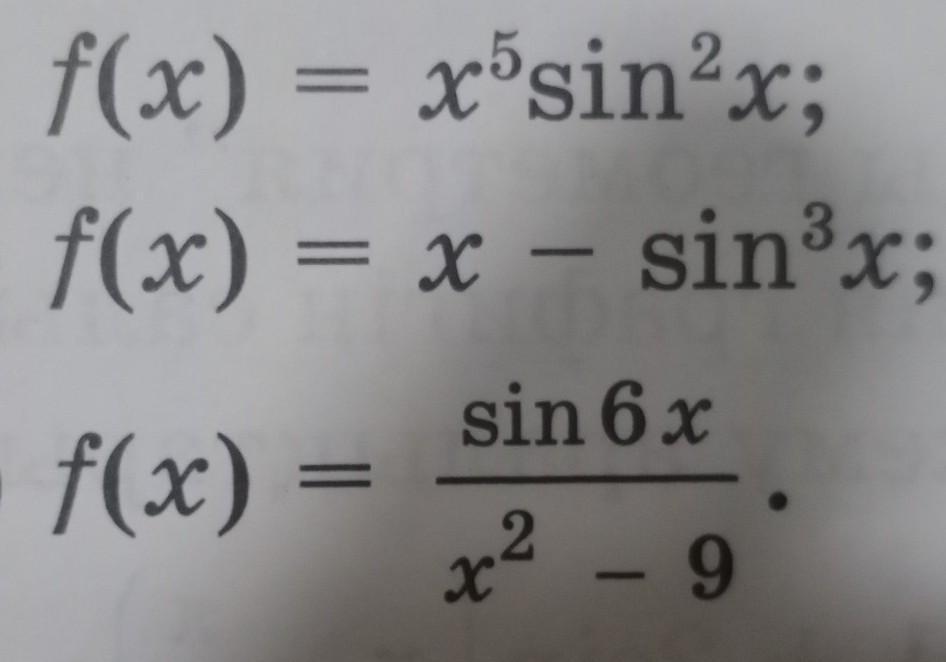Ответы
Ответ дал:
6
Ответ:
Можно доказать, что произведеие нечетной и четной функции - нечетная функция, сумма, или разность нечетных - нечетная, частное нечетной и четной - нечетная. Исходя из этого доказывается нечетность данных функций
f(-x) = (-x)^5×(sin(-x))^2 = - x^5×(sin x) ^2 = - f(x)
f(-x) = - x - (sin(-x)) ^3 = - x + (sin x) ^3 = - f(x)
f(-x) = sin(-6x)/((-x)^2 - 9) = - sin 6x/(x^2 - 9) = - f(x)
anuarbekovmiras393:
Решение тоже как бы надо
да ладно это будет усно человек же тоже старался)
Нет рил решение надо
Мне
ну знаешь не знаю как у тебя в школе но у меня задали одно а спрашивают другое)
Спасибо большое
тебе спасибо)
Хм
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад