Точка O - середина диагонали BD четырехугольника ABCD. Прямая,
параллельная AC и проходящая через точку O, пересекает сторону AD в
точке M. Докажите, что отрезок CM делит четырехугольник ABCD на два
равновеликих многоугольника.
Решите, пожалуйста, с рисунком.
siestarjoki:
что это за каша?
скопировалось криво, исправил
Задача о делении четырехугольника пополам прямой через вершину. Это ее вариант.
Построить равновеликий треугольник и разделить его медианой. CM и будет этой медианой.
Ответы
Ответ дал:
0
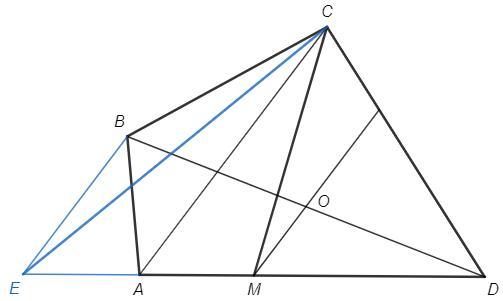
EB||AC
Расстояние между параллельными постоянно, треугольники AEC и ABC имеют равные высоты.
S(AEC)=S(ABC) => S(ECM)=S(ABCM)
OM||AC||EB, по теореме Фалеса точка M - середина ED
Медиана CM делит треугольник ECD пополам.
S(ECM)=S(MCD) =S(ABCM)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад