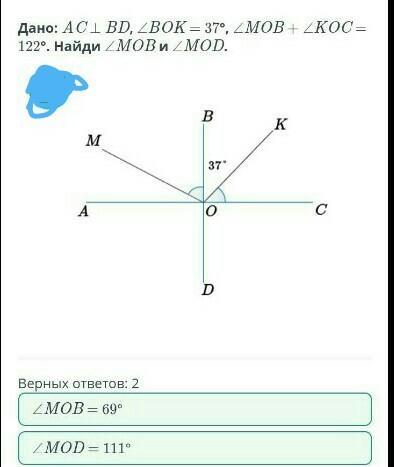
Дано: AC ⊥ BD, ∠BOK = 37°, ∠MOB + ∠KOC = 122°. Найди ∠MOB и ∠MOD.
У меня есть ответ, но мне нужно решение.
∠MOB - 69 ∠MOD - 111
Приложения:
Аноним:
А можно рисунок? И сколько ответ?
Сейчас отправлю фото
Нужно просто объяснить ход решения)
Ответы
Ответ дал:
1
Дано: AC ⊥ BD, ∠BOK = 37°, ∠MOB + ∠KOC = 122°.
Найти: ∠MOB и ∠MOD.
Решение:
Так как AC⊥BD, то при пересечении этих двух прямых образовалось 4 прямых угла:
∠AOB = ∠AOD = ∠DOC = ∠BOC = 90°
Угол ВОС поделен лучом ОК на два угла:
∠BOK + ∠KOC = ∠BOC
37° + ∠KOC = 90°
∠KOC = 90° - 37° = 53°; ∠KOC = 53°
По условию
∠MOB + ∠KOC = 122°
∠MOB + 53° = 122°
∠MOB = 122° - 53° = 69°; ∠MOB = 69°
Угол АОВ поделен лучом ОМ на два угла:
∠АOМ + ∠МOВ = ∠АOВ
∠АOМ + 69° = 90°
∠АOМ = 90° - 69° = 21°; ∠АOМ = 21°
∠МOD = ∠АOМ + ∠AOD = 21° + 90° = 111°
∠MOD = 111°
Ответ: ∠MOB = 69°; ∠MOD = 111°.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад