СРОЧНО!!!
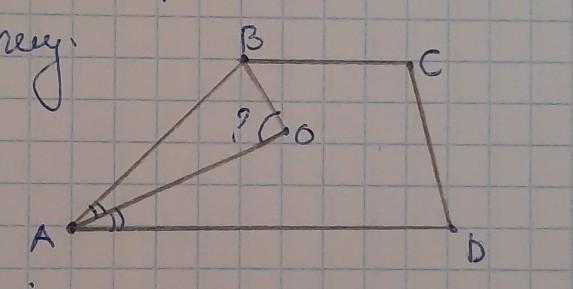
Дано: ABCD- трапеция.
АО-бис. угла ВАD
ВО-бис. угла СВА
найти: угол АОВ.
рисунок прикреплён
Приложения:
Ответы
Ответ дал:
15
Дано :
Четырёхугольник ABCD — трапеция (BC||AD).
AO — биссектриса ∠А.
ВО — биссектриса ∠В.
Найти :
∠АОВ = ?
Решение :
- В трапеции сумма двух углов, прилежащий к одной боковой стороне, равна 180°.
Следовательно ∠А + ∠В = 180°.
- Биссектриса угла — это луч, делящий угол на два равных угла.
Следовательно ∠ВАО = ∠ОАD, ∠ABO = ∠OBC.
Пусть ∠ВАО = ∠ОАD = х, а ∠ABO = ∠OBC = y.
Тогда :
х + х + у + у = 180°
2х + 2у = 180°
2(х + у) = 180° | : 2
х + у = 90°.
Рассмотрим ∆АОВ.
- Если в треугольнике сумма двух острых углов равна 90°, то этот треугольник — прямоугольный.
Так как х + у = 90°, то ∠АОВ = 90°.
Ответ :
90°.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад